تحلیل آماری در نتایج تحقیقات و مقالات مختلف از اهمیت بسیار زیادی برخوردار است. از این جهت استفاده از فرمول های تحلیل آماری به صورت صحیح و نحوه تفسیر هر یک از تست های آماری بسیار حائز اهمیت بوده و به غیر از اساتید باید دانشجویان نیز در مورد آن ها اطلاعات کسب کنند. تکنیک های تحلیل آماری شامل خطا، میانگین، تست فرضیه و رگرسیون هستند که هر کدام نتایج متفاوتی را در اختیار قرار می دهند. در این مقاله از سایت انجام پروژه های دانشجویی ، هر یک از این تکنیک ها را به صورت کامل بررسی میکنیم.
معرفی تکنیک ها و فرمول های تحلیل آماری
تحلیل های آماری به مجموعه ای از تکنیک ها گفته می شوند که با وجود آن کسب و کارها می توانند متوجه شوند که داده های بدست آمده آن ها با یکدیگر مرتبط هستند یا خیر. این موضوع نه تنها در دنیای تجارت و کسب و کارها بلکه در زمینه های مختلف تحقیقاتی نیز از اهمیت بسیار زیادی برخوردار بوده و باید با دقت مورد بررسی قرار گیرد. فرمول های تحلیل آماری امکان محاسبه نتایج آماری و رابطه میان متغیرها را می دهد که در ادامه به 4 روش اصلی آن اشاره می کنیم.
فرمول های تحلیل آماری
به منظور تحلیل آماری داده های مختلفی وجود دارند که باید هر یک از آن ها را مد نظر داشت. نه تنها دانشجویان، بلکه برای کسب و کارها و مشاغل مختلف نیاز به تحلیل های آماری مختلفی است که هر یک از آن ها را باید مد نظر داشت. از جمله مهمترین فرمول های تحلیل آماری می توان به موارد زیر اشاره کرد:
1. میانگین
میانگین سادهترین تکنیک برای تحلیل آماری است. با داشتن میانگین و متوسط می توانید متوجه شوید که عملکرد داده های شما به صورت میانگین چگونه بوده اند. نحوه محاسبه میانگین نیز بسیار ساده است. فقط کافیست همه داده های مورد نظر خودتان را با یکدیگر جمع کرده و سپس تقسیم بر تعداد کنید. این روش می تواند به شما این امکان را بدهد تا نقطه مرکزی یک مجموعه داده را تعیین کنید. فرمول میانگین به شرح زیر است.
مزایا و معایب میانگین
میانگین برای داده هایی قابل استفاده است که امکان جمع کردن آن ها وجود داشته باشد. محاسبه میانگین بسیار ساده بوده و این خود یک مزیت بزرگ برای آن محسوب می شود. علاوه بر این، درک میانگین بسیار ساده است. به طوری که نشان می دهد بقیه مقادیر چقدر با میانگین فاصله دارند. با این حال معایب میانگین نیز این است که احتمالا به دلیل وجود مقادیر پرت دچار انحراف می شود. با وجود اینکه در 80 درصد مواقع میانگین به خوبی عمل می کند، اما در 20 درصد مواقع نیز نتایج خوبی را ارائه نمی کند.
برخی خدمات ما در این زمینه:
جالب است بدانید در زمان انجام مقاله isi بسیاری از رشته ها، از تحلیل آماری استفاده میشود. اگر مقاله isi شما هم نیاز به تحلیل آماری دارد، میتوانید از خدمات کارت پروژه در این زمینه کمک بگیرید. علاوه بر این، خدمات زیر هم توسط تیم ما ارائه میشوند:
انجام پروژه spss | انجام پروژه تحلیل آماری | انجام پروژه آمار
انجام پروژه روش تحقیق | انجام پروژه R | سفارش طراحی پرسشنامه
2. انحراف معیار
انحراف معیار یکی از مهمترین فرمول های تحلیل آماری است که می توان برای تعیین پراکندگی نقاط داده استفاده کرد. این روش تجزیه و تحلیل آماری مهمی بوده که نشان می دهد در اطراف میانگین هر گروه از داده چگونه داده ها منتشر شده اند. هر چقدر انحراف معیار پایینتر باشد، نشان می دهد که داده ها بیشتر به میانگین نزدیک هستند. این اعتبار داده ها را نشان می دهد.
به طور مثال در یک پرسشنامه که سوالات مشابهی وجود دارند اگر درصد زیادی از سوالات پاسخ مشابهی داشته باشند، انحراف معیار به دست آمده پایینتر بوده و امکان استفاده از آن ها برای جمعیت بزرگتر وجود دارد. فرمول انحراف معیار به شرح زیر است:
که در این فرمول:
- σ نشان دهنده انحراف معیار است.
- Σ مجموع داده ها (جمع آن ها) را نشان می دهد.
- x مقدار مجموعه داده را نشان می دهد.
- μ میانگین داده ها را نشان می دهد.
- n تعداد نقاط داده در جامعه و گروه مورد نظر را مشخص می کند.
نحوه تفسیر انحراف معیار
انحراف معیار یکی از شاخص های پراکندگی است که نشان می دهد به صورت میانگین داده ها چقدر از مقدار متوسط یا همان میانگین فاصله دارند. نحوه تفسیر به این شکل است که اگر انحراف معیار مجموعه ای از داده ها نزدیک به صفر باشند، نشان می دهد که داده ها بسیار نزدیک به میانگین هستند و پراکندگی آن ها بسیار کم است؛ اما اگر انحراف معیار بزرگ باشد، پراکندگی قابل توجه داده ها را نشان می دهد.
مزیت انحراف معیار نسبت به واریانس این است که هم بعد با داده ها می باشد. از این جهت می توان از انحراف معیار برای تعیین ضریب اطمینان را در تحلیل های آماری استفاده نمود. در تحلیل های آماری در صورتی که داده ها با اختلاف بیشتر از دو انحراف معیار از مقدار میانگین باشند، به عنوان داده های پرت در نظر گرفته می شوند و از پروسه تحلیل خارج می شوند.
3. رگرشن یا رگرسیون
یکی دیگر از فرمول های تحلیل آماری که برای پیدا کردن رابطه میان یک متغیر وابسته و یک متغیر مستقل استفاده می شود، رگرسیون است. با داشتن این تحلیل آماری می توانید متوجه شوید که چگونه تغییرات یک متغیر بر تغییرات یک متغیر دیگر تاثیر می گذارد. بنابراین، عدد بدست آمده نشان می دهد که آیا رابطه میان دو متغیر ضعیف یا قوی است یا اینکه در بازه زمانی مختلف تغییر می کند یا خیر. در زیر فرمول رگرسیون را مشاهده می کنید.
که در این فرمول:
- Y متغیر مستقل یا داده های مورد استفاده برای پیش بینی متغیر وابسته را نشان می دهد.
- x متغیر وابسته است را نشان می دهد که متغیری است که می خواهید اندازه گیری کنید.
- a وقفه یا مقدار y زمانی است که x برابر با صفر باشد را نشان می دهد.
- b شیب نمودار رگرسیون را نشان می دهد.
4. تست فرضیه
یکی از فرمول های تحلیل آماری که با نام آزمون فرضیه نیز شناخته می شود، یکی از روش های آماری است. در این روش می توان متوجه شد که نتیجه گیری برای یک مجموعه از داده های خاص با مقایسه داده ها در برابر یک فرض خاص معتبر هست یا خیر. نتیجه آزمون می تواند باعث باطل کردن فرضیه شود که به آن فرضیه 0 می گویند. علاوه بر این باید توجه داشت که هر چیزی که فرضیه صفر را نقص کند، فرضیه اول یا فرضیه 1 نام دارد.
نحوه تفسیر
هر آزمون فرضیه دارای دو فرضیه است: فرضیه صفر و فرضیه جایگزین. اگر نتیجه صفر باشد، هیچ رابطه ای بین نمونه ها وجود دارد؛ ولی فرضیه صفر وجود یک رابطه را نشان می دهد. بنابراین، آزمون فرضیه می تواند هر دو احتمال را در نظر بگیرد.
فرضیه صفر
فرضیه صفر نشان می دهد که هیچ رابطه ای در پارامترهای متغیری که اندازه گیری شده اند وجود ندارد. بنابراین، هیچ رابطه معناداری میان متغیرها وجود نداشته و اگر آزمون چندین بار تکرار شوند، نتایج متفاوت خواهند بود.
فرضیه جایگزین
فرضیه جایگزین در نقطه مقابل فرضیه صفر قرار می گیرد. زمانی که فرضیه صفر رد می شود، فرضیه جایگزین به صورت خودکار انتخاب می شود و ما نقشی در انتخاب یا عدم انتخاب آن نداریم. این نوع فرضیه نشان می دهد که میان متغیرهای موجود ارتباط معناداری وجود دارد. خود این ارتباط می تواند به صورت جهت دار و غیر جهت دار باشد.
- جهت دار: فرضیه جایگزین جهت دار می تواند نوع رابطه میان متغیرها را مشخص کند. به طور مثال، اینکه یک متغیر کمتر از متغیر دیگر است و موارد این چنینی.
- غیر جهت دار: فرضیه جایگزین غیر جهت دار نشان می دهد که میان نمونه های اندازه گیری شده از نظر آماری تفاوت معناداری وجود دارد. ولی هیچ گاه بیان نمی کند که کدام یک نسبت به دیگری برتری دارد، فقط نشان می دهد که آن ها با یکدیگر متفاوت اند.
تحلیل آماری در رشته های مختلفی کاربرد دارد. در لیست زیر خدماتمان در بعضی از این رشته ها را لیست کرده ایم:
انجام پروژه داده کاوی | انجام پروژه دیتاساینس | انجام پروژه روانشناسی
انجام پروژه علوم تربیتی | انجام پروژه علوم اجتماعی | انجام پروژه مینی تب
سخن پایانی
در این مقاله در مورد فرمول های تحلیل آماری با شما صحبت کردیم. با توجه به اینکه تحلیل آماری یکی از مباحث بسیار مهم در حوزه های مختلف به ویژه درسی و دانشجویی است، باید با دقت تمام انجام شود. میانگین، انحراف معیار، رگرسیون و فرضیه چهار فرمول تحلیل آماری هستند که هر کدام مفاهیم متفاوتی را در اختیار قرار می دهند. طبق توضیحات داده شده بسته به اینکه چه نوع متغیری را نیاز به بررسی و مقایسه داریم، باید از فرمول های تحلیل آماری مناسب استفاده کنیم.
حال که به موضوع “فرمول های تحلیل آماری” علاقه دارید، مقالات زیر هم میتوانندبرای شما جذاب باشند:
- نرم افزار تحلیل داده های کیفی (+ مقایسه این نرم افزارها)
- تحلیل آماری چند متغیره و پاسخ به 3 سوال پر تکرار
- تجزیه و تحلیل داده ها با هوش مصنوعی
- انواع روشهای تحلیل آماری:معرفی 8 روش مختلف
سوالات متداول
واریانس بهتر است یا انحراف معیار؟
انحراف معیار از توان دوم واریانس بدست می آید و می تواند نتایج دقیقتری را برای تحلیل آماری در اختیار قرار دهد.
آیا میانگین برای تحلیل آماری کافیست؟
خیر با داشتن میانگین نمی توان به طور دقیق مشخص کرد که چقدر داده ها به میانگین نزدیک اند و آیا می توان به آن ها استناد کرد یا خیر.
آیا رگرسیون برای تخمین داده ها مناسب است؟
بله. به دلیل اینکه رگرسیون یک معادله خط را در اختیار قرار می دهد، می تواند برای تخمین داده ها و پیش بینی آن ها جهت استفاده در آینده استفاده شود.






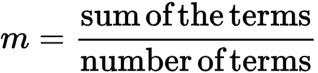
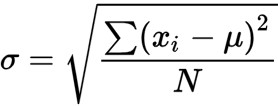
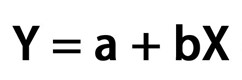




ارسال پاسخ