در این دوره آنلاین آموزش متلب به صورت رایگان با سری آموزشهای نرم افزار متلب در خدمت شما هستیم. در واقع آنچه که شما به طور کاملا عملی برای استفاده در انجام پروژه متلب نیاز دارید در این جلسات ارائه خواهد شد.
دستور prod در متلب
در جلسه گذشته در رابطه با دستور sum در متلب صحبت کردیم. در این جلسه میخواهیم با نحوه محاسبه ضرب عناصر یک ماتریس در متلب آشنا شویم.
دستور prod در متلب، برای محاسبه ضرب عناصر ردیفها یا ستونهای یک ماتریس به کار می رود.
حال اگر ما به طور مثال حاصلضرب همه درایههای ماتریس B را بخواهیم، چگونه باید آن را به دست آوریم؟
یک تابعی به نام product داریم یعنی اگر به صورت prod (B) بنویسیم، حاصل ضرب ماتریس در متلب آن را به ما میدهد.
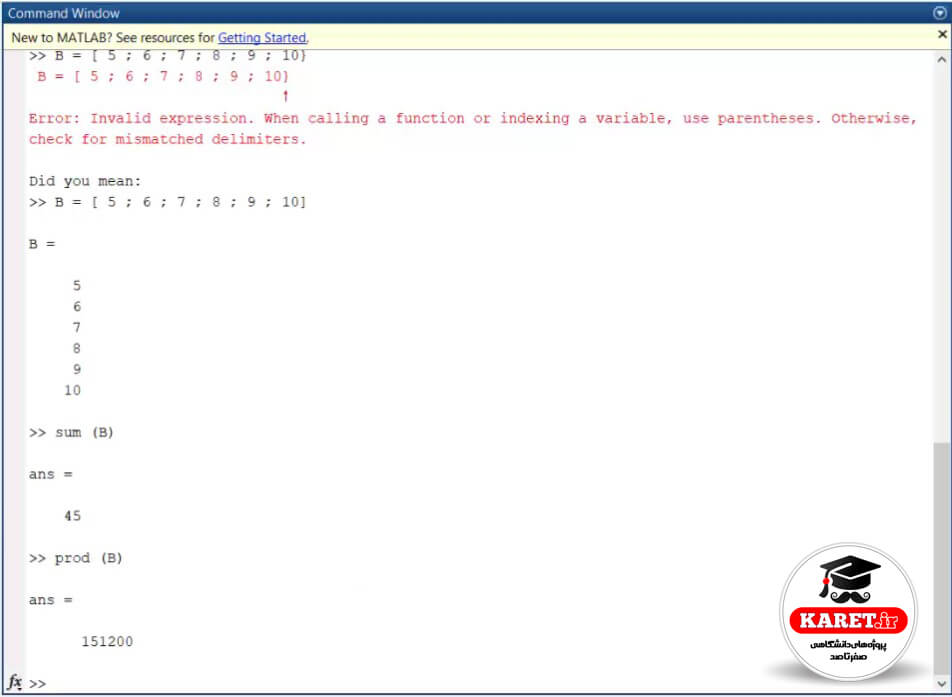
اگر بخواهیم مجموع اعداد را در یک rangeای به دست آوریم. جمع اعداد متوالی در ریاضیات یک فرمولی دارد و فرمول آن هم این است که (عدد اول بهاضافهی عدد آخر) ضربدر کل اعداد و سپس بر ۲ تقسیم میشود. حال فرض کنید که ما از مجموع اعداد از محدودهی ۱ تا ۲۰ را به دست آوریم. عدد اول ما که ۱ است، با عدد آخر یعنی ۲۰ جمع میشود و حاصل جمع ۲۱ میشود. این حاصل ۲۱ ضربدر تعداد کل اعداد یعنی ۲۰ میشود و جواب حاصلضرب بر عدد ۲ تقسیم میشود که نتیجه نهایی جواب ۲۱۰ را به ما میدهد.
حال ما میخواهیم این تابع را تعریف کنیم. در جلسه دهم (دستور range در متلب) گفتیم range به صورت a:b تعریف میشود.
در اینجا میخواهیم 1:20 را به دست آوریم.
در بالا توضیح دادیم که در ریاضیات این حاصل جمع چگونه به دست میآید که جواب ۲۱۰ میشود.
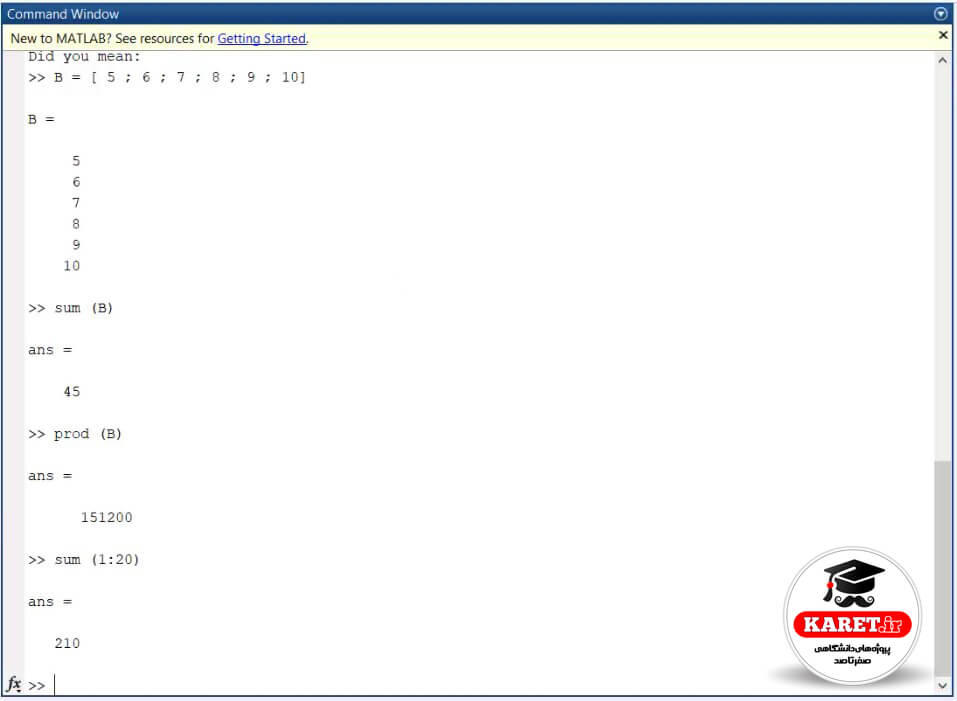
جواب چگونه به دست آمد؟ عدد اول آن ۱ بود به اضافهی عدد آخر یعنی ۲۰ شد که میشود ۲۱. ضربدر کل اعداد که ۲۰ تا است، شد و بعد بر ۲ تقسیم شد که برابر میشود با ۲۱۰. به سادگی میتوان آن را در rangeهای مختلف به دست آورد.
ما در ریاضیات یک مفهوم فاکتوریل داشتیم. به نظر شما با rangeای که توضیح دادم، فاکتوریل چگونه به دست میآید؟
به طور مثال میخواهیم بدانیم که در اینجا !8 را با استفاده از نکاتی که در بالا به آن اشاره کردیم، چگونه میتوانیم به دست آوریم؟
به راحتی آن را به صورت زیر مینویسیم:
Prod (1:8)
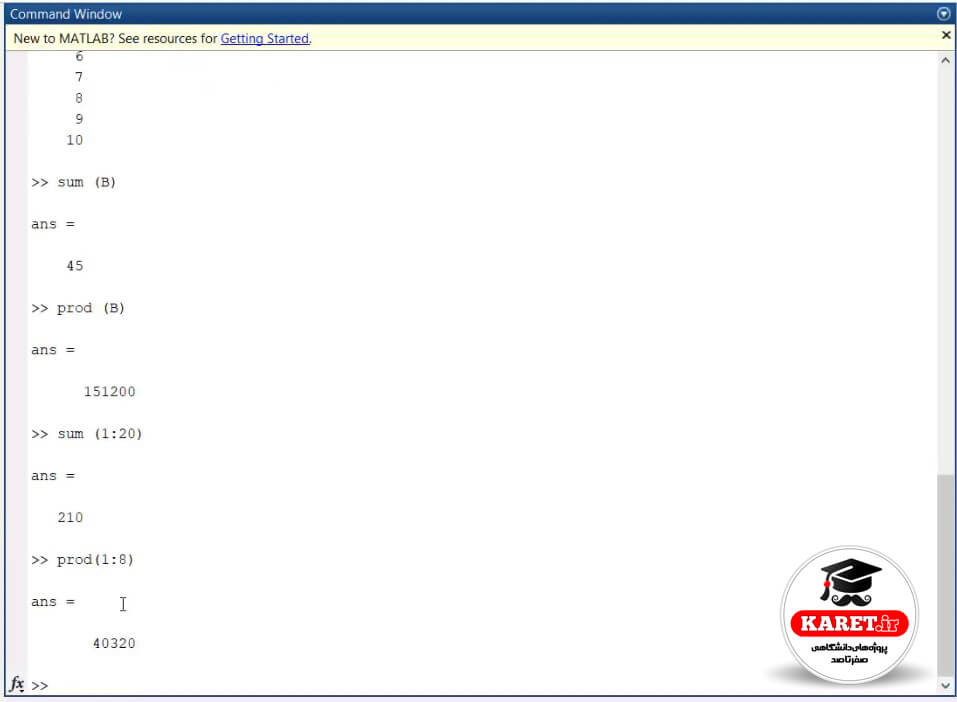
که جواب !8 را برای ما به دست میآورد.
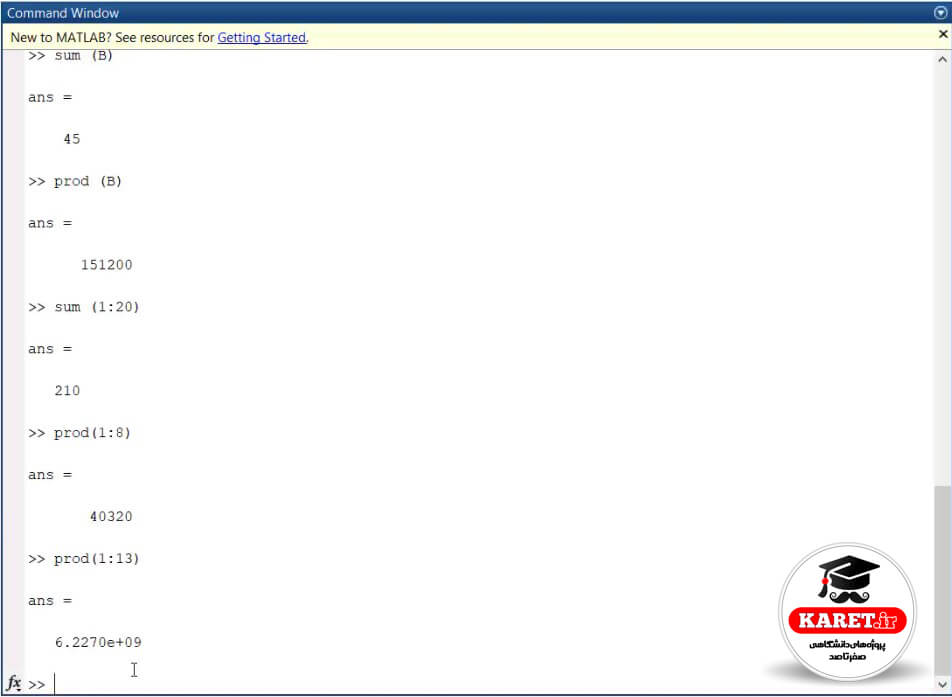
حال اگر بخواهیم !13 را به دست آوریم به صورت زیر مینویسیم و جواب به سادگی به دست میآید.
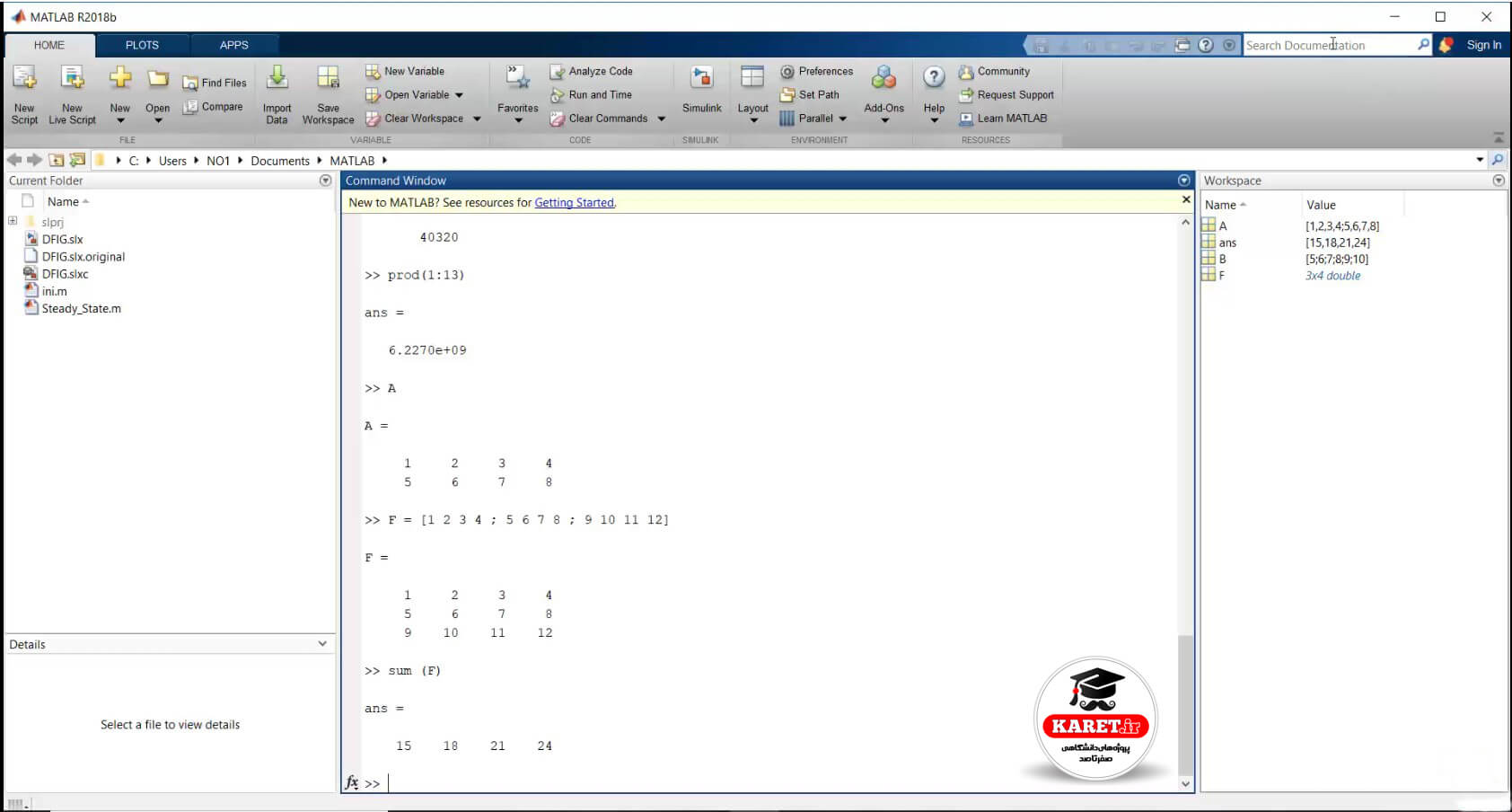
ما در انتهای جلسه چهارم (پنجره command history در متلب) یک ماتریس A را تعریف کردیم که به صورت زیر نوشته شده بود.
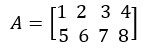
در اینجا میخواهیم ماتریس دیگری به نام F به صورت زیر تعریف کنیم و سطر که سطر سوم آن را در A حذف کرده بودیم ولی باز سطر سوم آن را آوردیم.
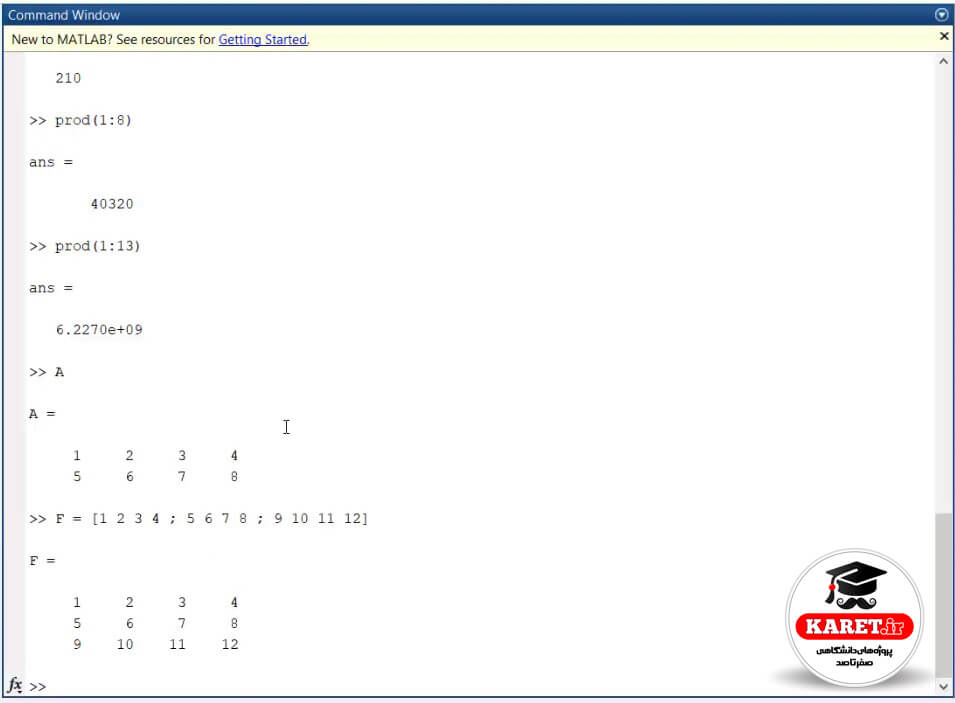
میتوان با آن جمع هم انجام داد که بعدا توضیح میدهم.
در اینجا در ماتریس F میخواهیم ببینیم وقتی که sum (F) را بزنیم، در ماتریس به چه صورت درمیآید. با توجه به چیزی که پیشتر آموختید sum (F) چگونه اینها را جمع میکند؟
پاسخ را در تصویر زیر مشاهده میکنید.
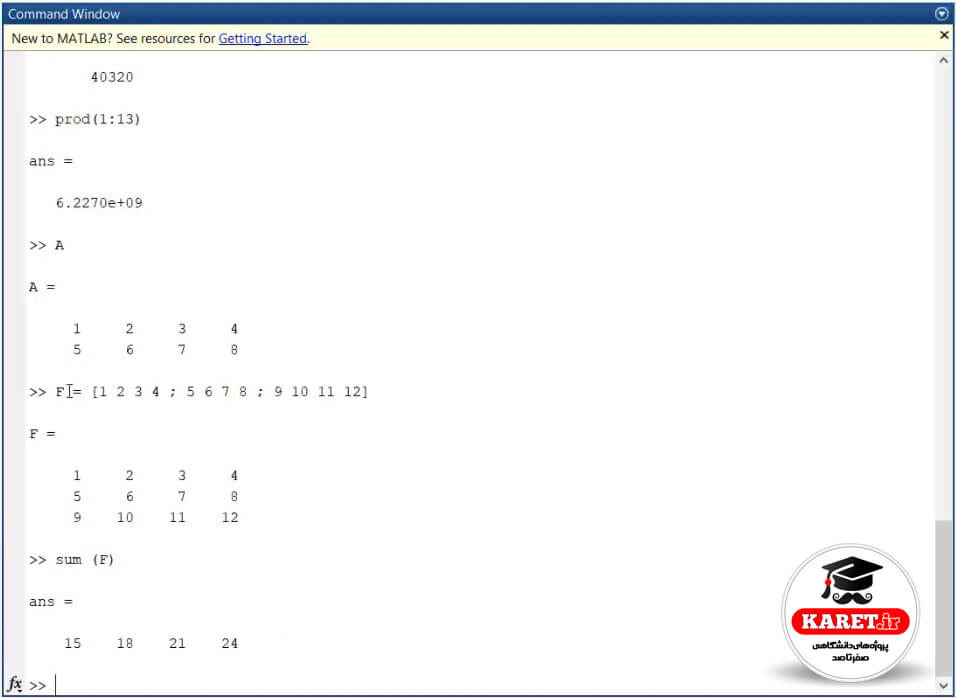
گفته بودیم که اولویت با سطر است، پس در هر سطر، درایههای متناظر را با هم جمع کرده است (یعنی درایهی اول در سطر اول و دوم و سوم را با هم جمع کرده است) و درایهی اول در ماتریسِ حاصل، 15 = 9 + 5 + 1 شده است.
سپس درایههای دوم از هر سطر را با هم جمع کرده است که حاصل 18 = 10 + 6 + 2 شد و به ترتیب برای درایههای دیگر یعنی درایههای سوم و چهارم پاسخهای 21 = 11 + 7 + 3 و 24 = 12 + 8 + 4 به دست میآید.
حال شما میتوانید در مورد sum هم در این قسمت search برنامهی متلب جستوجو کنید و ببینید چه چیزهایی در مورد آن وجود دارد و هم میتوانید بگویید…
بریم سراغ ادامهی نکات دربارهی تابع sum:

همانطور که گفتیم، اگر بخواهیم به اطلاعات یک تابع دست پیدا کنیم و ببینیم در مورد آن چه نکاتی وجود دارد، میتوانیم آن را در Documentation سرچ کنیم یا همینجا مثلاً میخواهیم راجع به تابع sum خود متلب چه اطلاعاتی به ما میدهد، مینویسیم doc sum.
اگر بر روی آن کلیک کنیم، یک صفحهای برای ما باز میشود که راجع به آن توضیح داده است.
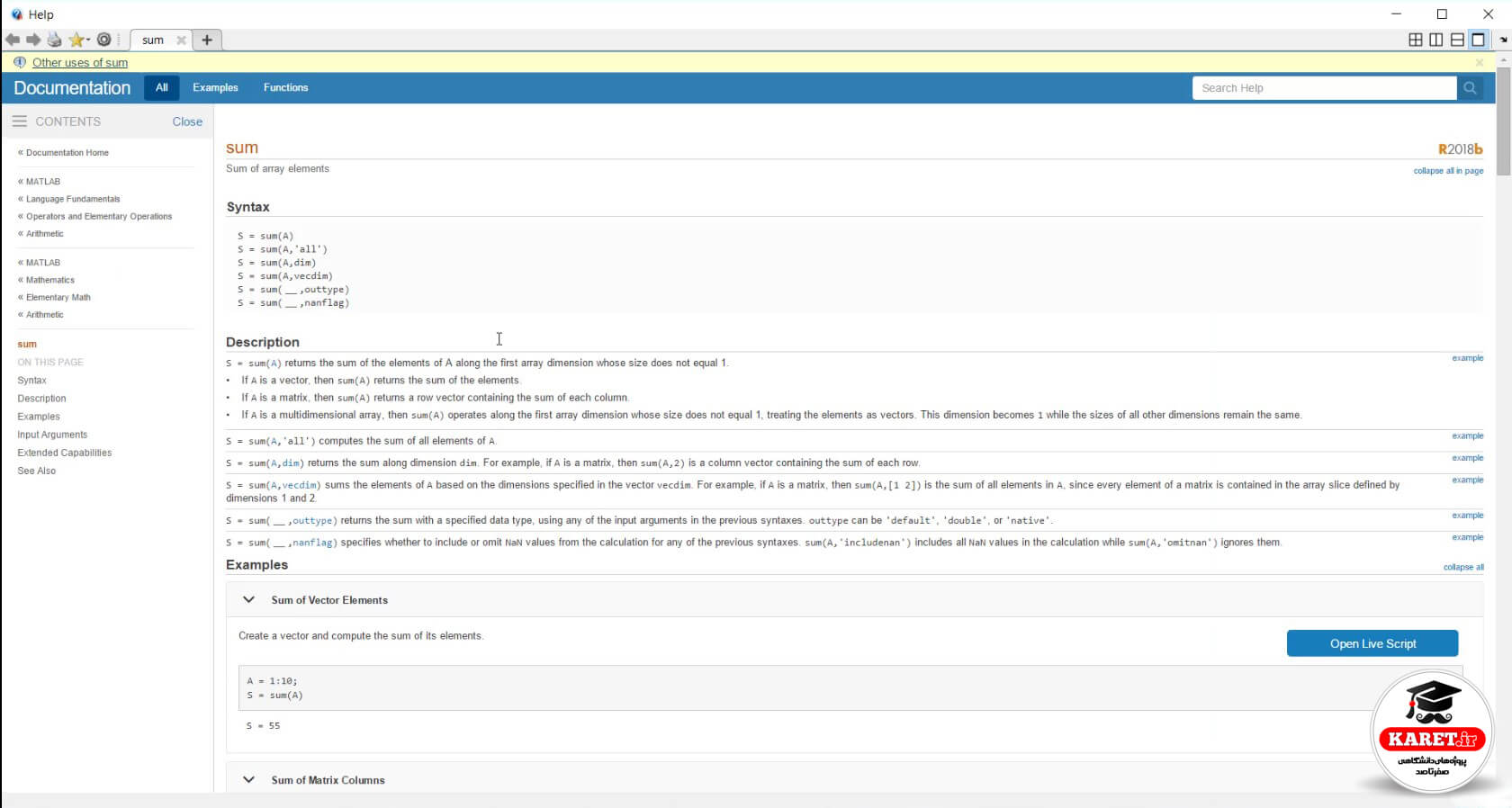
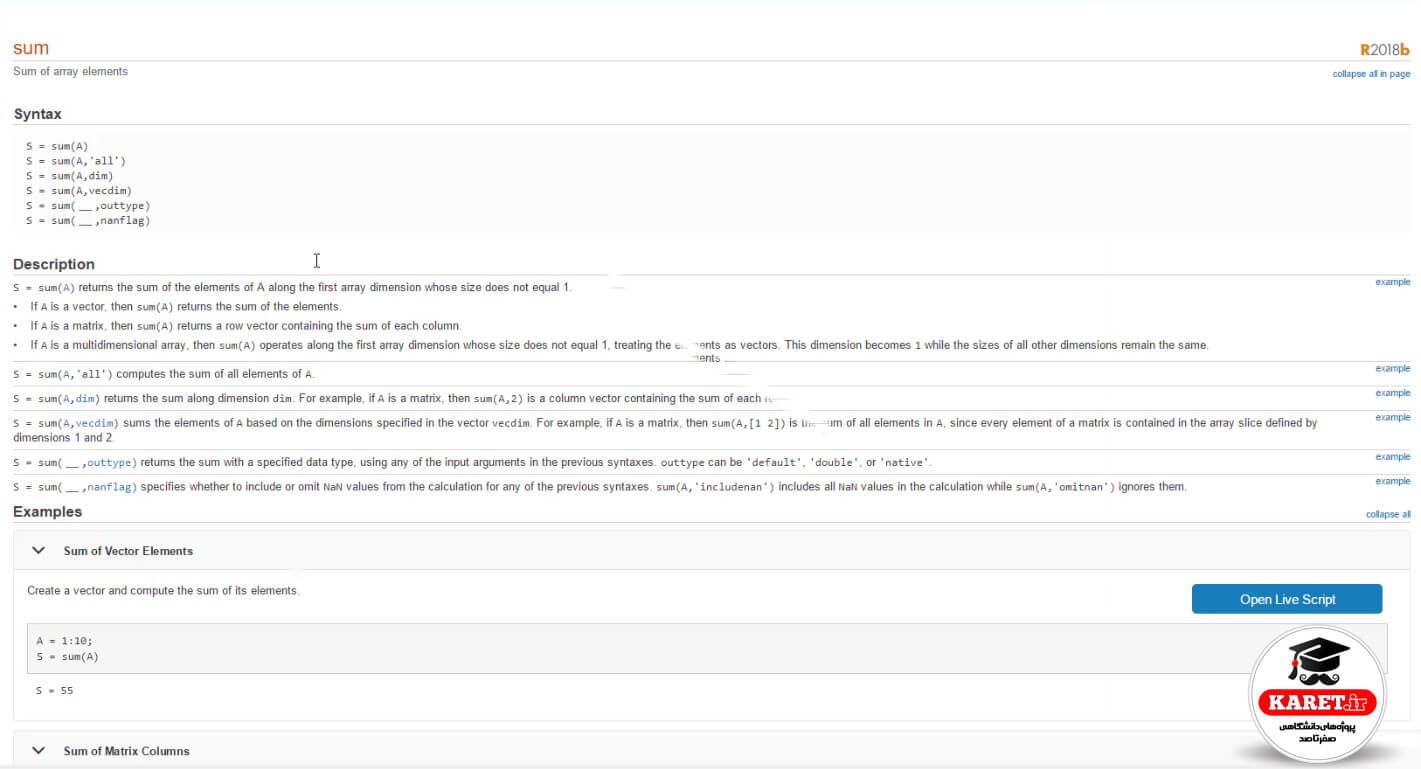
و برای مثال گفته است sum چیست و چه کاری انجام میدهد؛ گفته است sum pf array elements یعنی اینکه اعضا را با هم جمع میکند.
Syntaxها یعنی حالتهای مختلفی که برای آن هست را توضیح داده است که مثلاً این را برایتان توضیح دادم که مینویسید sum(A) یعنی sum ماتریس A تمام اعضا را با هم جمع میکند.
Sum(A,’all’) تمام اعضا را به صورت all یعنی تمام جمع میکند.
در Sum (A, ‘dim’)، dim مخفف dimension به معنی بُعد است.
مثلاً اگر بخواهیم این را برایتان توضیح دهم و شما راجع به آن چیزی ندانید، از این قسمت توضیحات را مطالعه میکنید. باید انگلیسی قوی داشته باشید.
گفته است که در راستای آن بُعد جمع را انجام میدهد که بُعد همان dim است. برای مثال اگر بخواهیم مثال بزنیم، اجازه دهید که در این قسمت برایتان مثال میزنم.
برای مثال ماتریس A را داریم که به صورت زیر است:
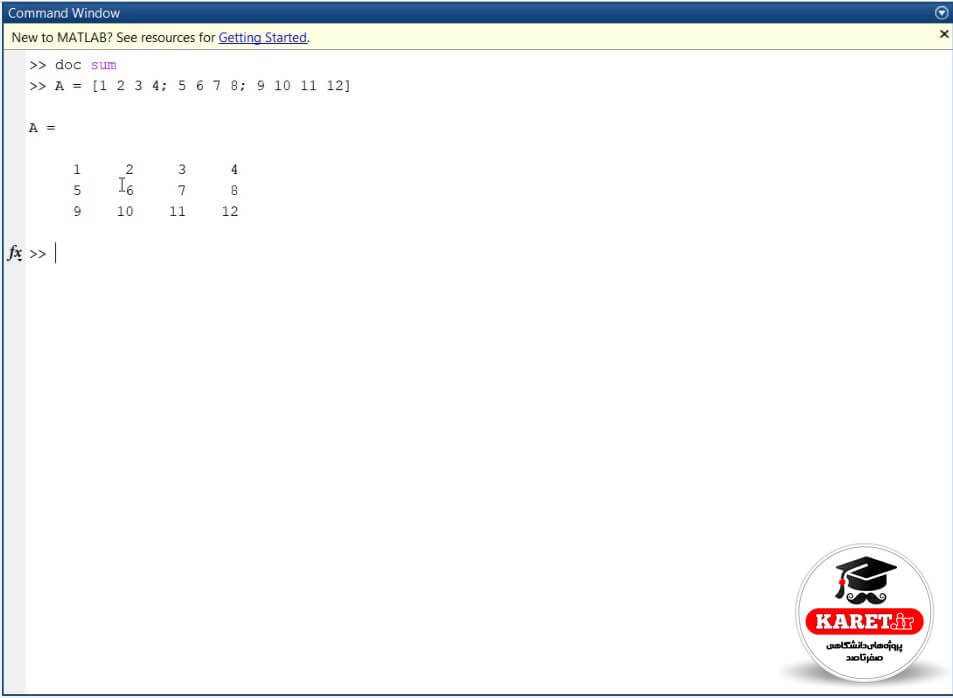
این ماتریس دارای ۴ ستون و ۳ سطر است. حال اگر بنویسیم sum (A) همانطور که بالاتر طبق تصویر برایتان توضیح دادم، در راستای سطح اینها را جمع میکند.
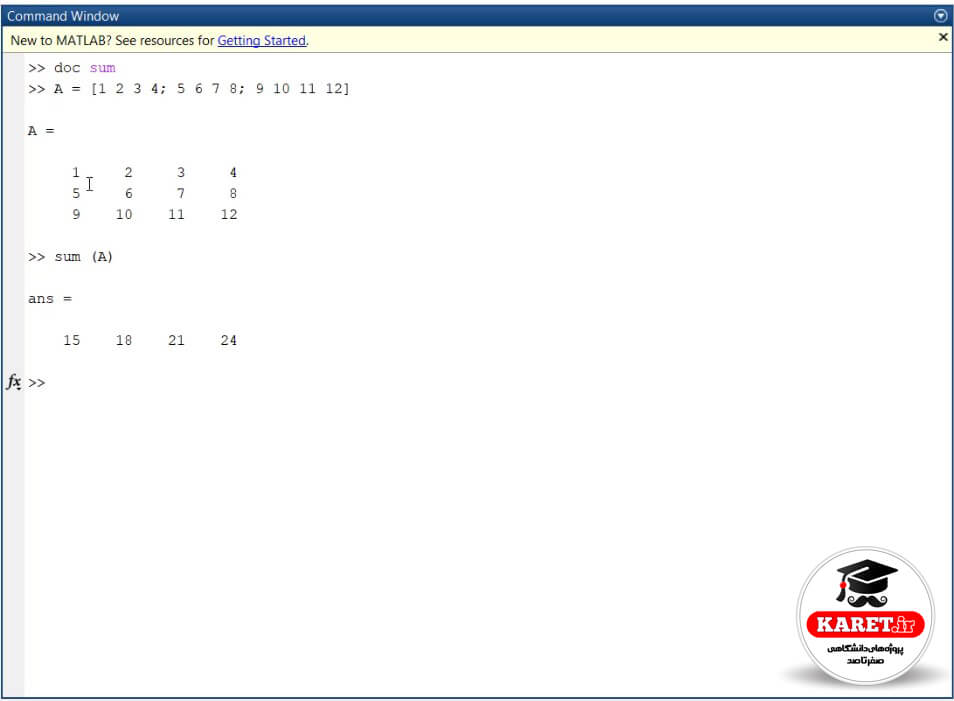
که عدد ۱ مربوط به مؤلفهی 1,1 است. ۲ مربوط به مؤلفهی 1,2 است یعنی سطر ۱ و ستون ۲. به صورت سطری اینها را جمع میکند و در جواب مینویسد.
اگر به طور مثال بنویسیم sum (A, 1) یعنیsum (A) و dimension (بُعد) اول که همان سطر است، مشاهده میکنید که جواب مشابه قبلی است.
حال اگر بنویسیم sum (A, 2) یعنی sum A و dimension (بعد) دوم یعنی ستون؛ یعنی بر اساس ستون جلو بیاید یعنی روی ستونها حرکت کند و جمع کند، به این صورت میشود:
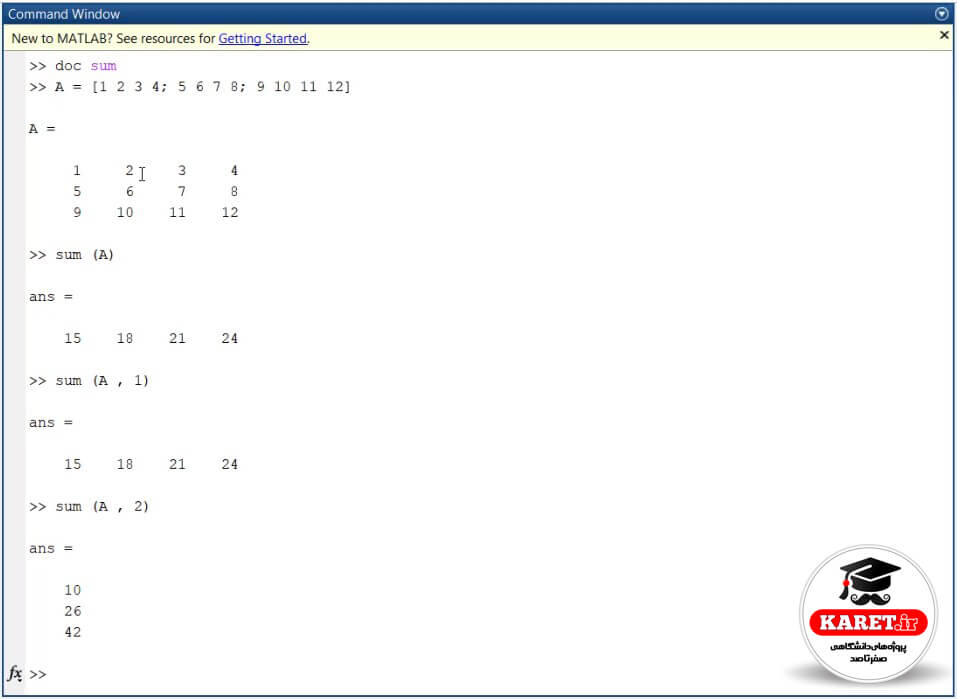
اگر به صورت ستونی جلو برود 10 = 4 + 3 + 2 و یک ستون کلی را به ما میدهد. اگر میخواهید در یاد داشته باشید، 2 یعنی ستون پس یک ستون را به ما میدهد و 1 یعنی سطر و یک سطر را کلا به ما میدهد.
حال اگر بخواهیم اعضای sum را به صورت کلی جمع کنیم، یک روش این است که بگویید sum(A) که در بالا هم نوشته بودیم که جواب 24 21 18 15 بود.
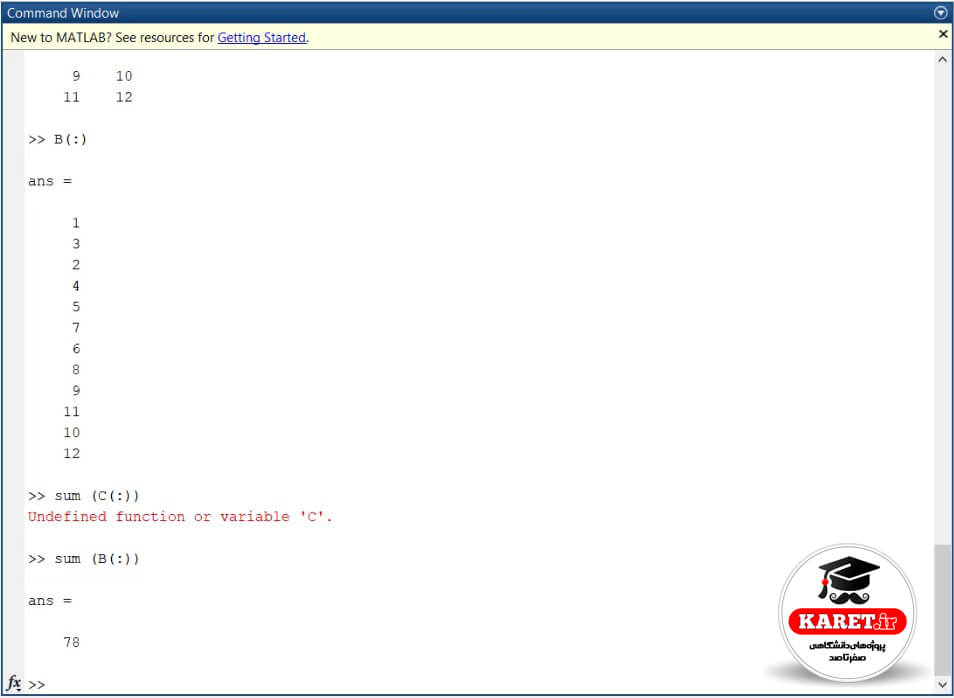
بار دیگر به صورت sum (sum(A)) بنویسیم و آن را هم محاسبه کنیم که جواب به صورت زیر است:
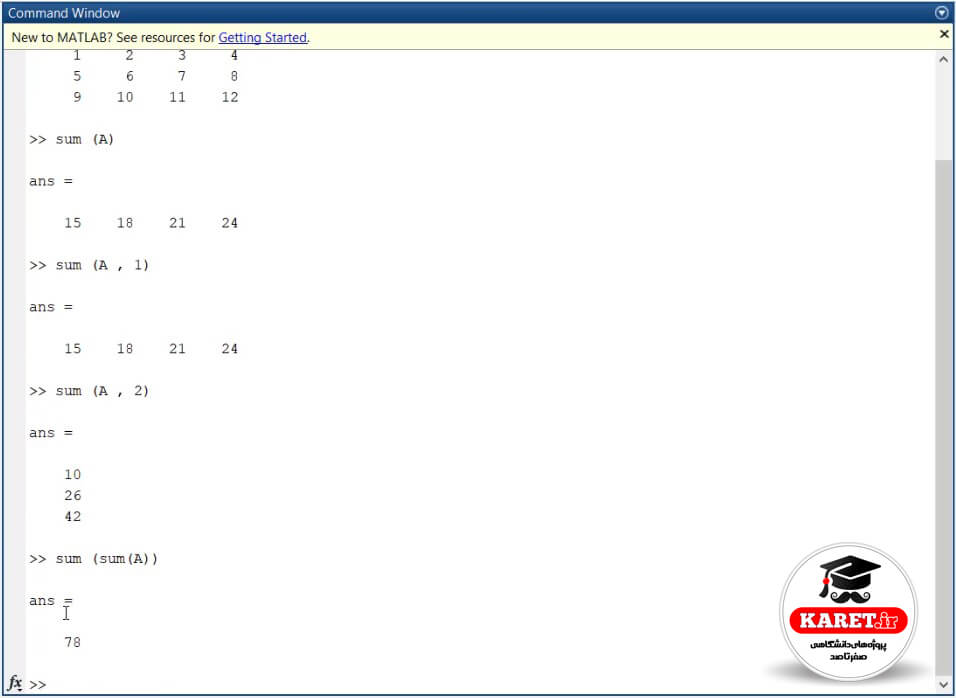
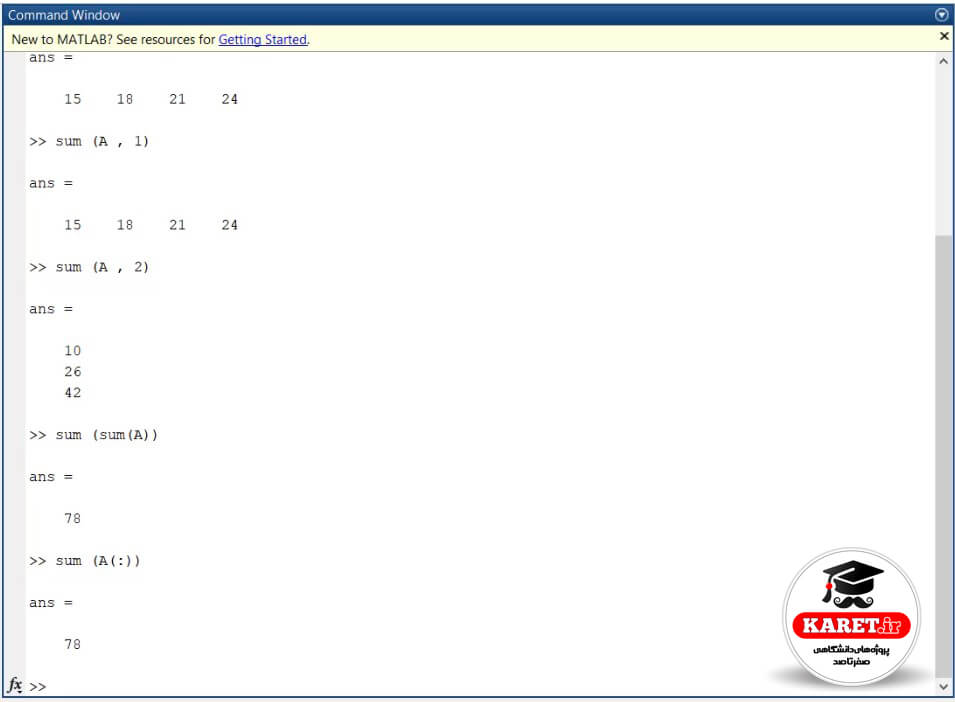
که جواب ۷۸ را به ما داده است ولی این روش، روش جالبی نیست. میتوانیم بگوییم sum(A) تمام اعضای آن: که قبلاً هم گفتیم تمام اعضا را به صورت زیر نشان میدهیم که باز همان جواب ۷۸ را به ما میدهد.
حال میخواهیم تعریف کنیم و کمکم در مورد ماتریسهای سهبعدی هم تعریف میشود. همانطور که گفتیم dimension را تا ۲ بُعد میآورید، ۳ بُعدی آن را هم میتوانیم داشته باشیم. برای مثال میگوییم که ماتریس B را تعریف میکنیم، میگوییم همهی سطرها … همهی ستونهای بعد اول که همان سطر میشود، برابر است با [4 3 ; 2 1]. مشاهده میکنید که در بُعد اول B به صورت زیر نشان داده میشود.
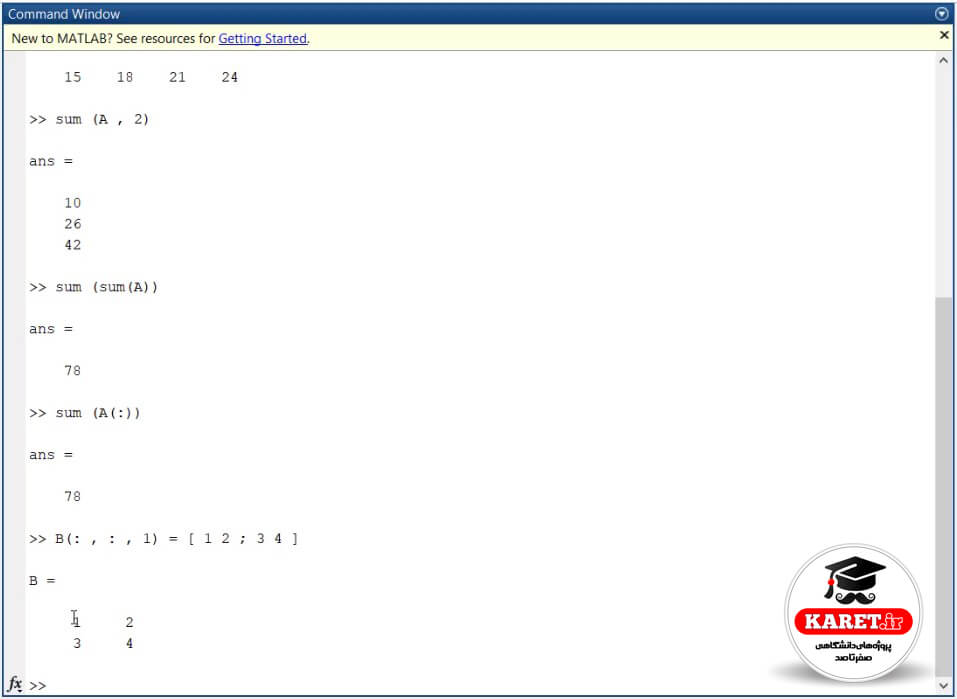
اکنون میگوییم همهی سطرها و همهی ستونها در بعد دوم برابر است با [8 7 ; 6 5].
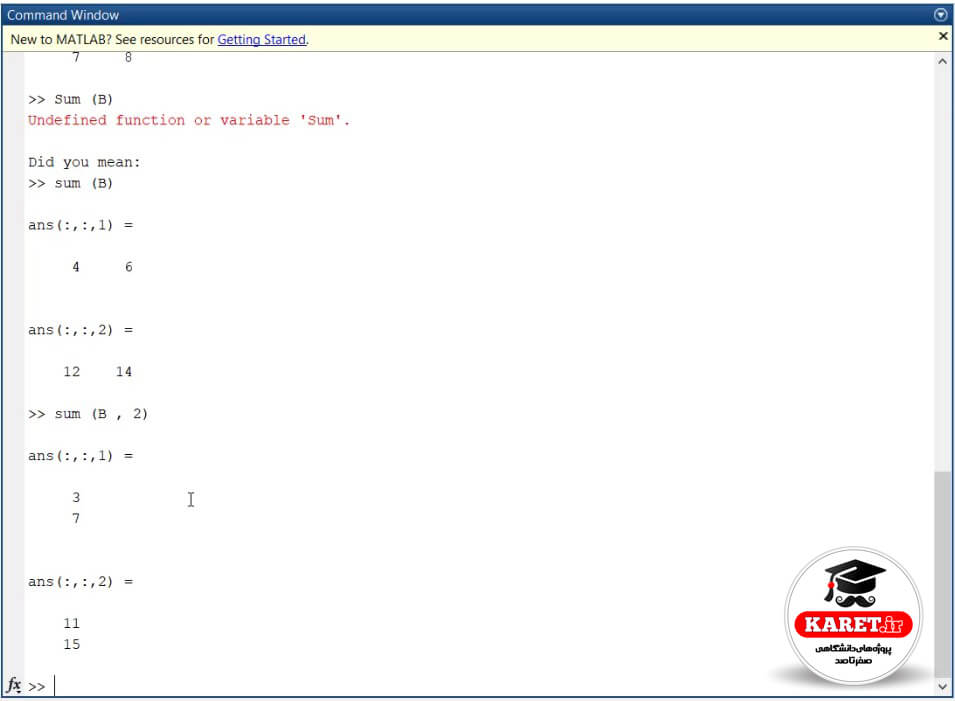
حال میخواهیم جمع اینها را ببینیم که چگونه است. مینویسیم sum(B). وقتی sum(B) خالی را بگویید، همان در راستای سطرها میشود. در اینجا اشتباه گرفت به دلیل اینکه از S بزرگ استفاده کردیم.
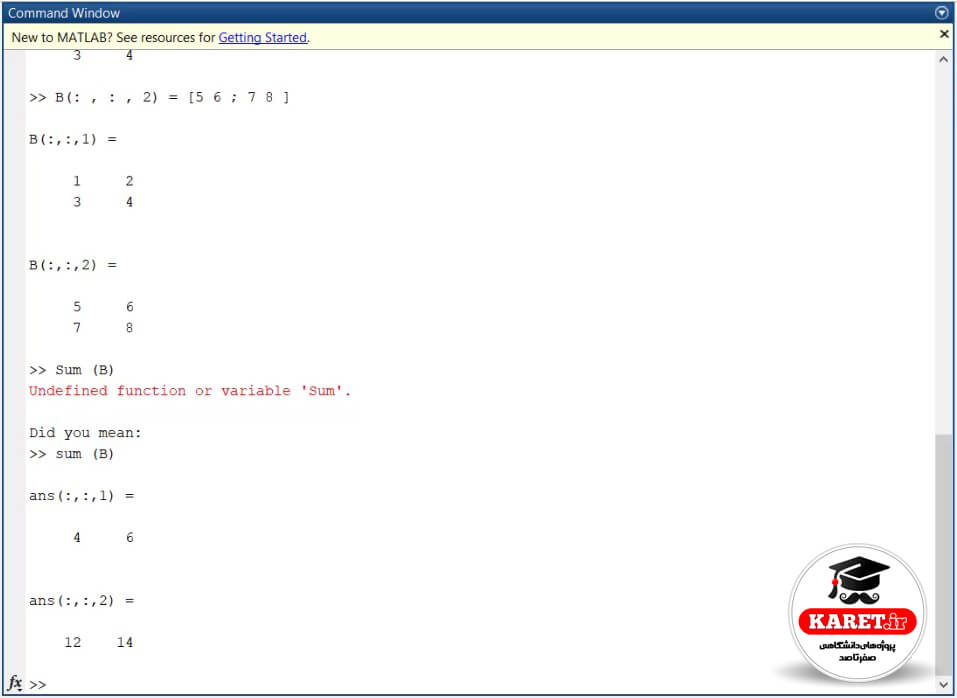
میخواهیم ببینیم جواب چگونه به دست آمد. گفتیم که در راستای سطرها با هم جمع کند. به سادگی میگوید که 4 = 3 + 1 و 6 = 4 + 2 و 12 = 7 + 5 و 14 = 8 + 6.
حال میخواهیم بگوییم که در راستای ستونها جمع را انجام دهد. مینویسیم sum(B, 2) یعنی sum B در راستای ستونها که بُعد دوم میشود. همانطور که مشاهده میکنید پاسخ به صورت زیر نشان داده میشود.
دو ماتریس زیر چگونه به دست آمدند؟

در ماتریس زیر داریم 3 = 2 + 1 و 7 = 4 + 3
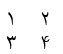
که ستون آن به صورت زیر به دست میآید.
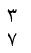
در صورتی که بخواهیم طبق روش بالا ماتریس زیر را محاسبه کنیم به صورت مقابل مینویسیم: 11 = 6 + 5 و 15 = 8 + 7
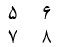
که جواب زیر به دست میآید.
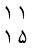
حال اگر بگوییم sum B و بعد سوم، (sum(B, 3)) به نظر شما جواب چگونه خواهد بود و آن را چگونه جمع میکند؟
جواب در اینجا به صورت زیر میباشد:
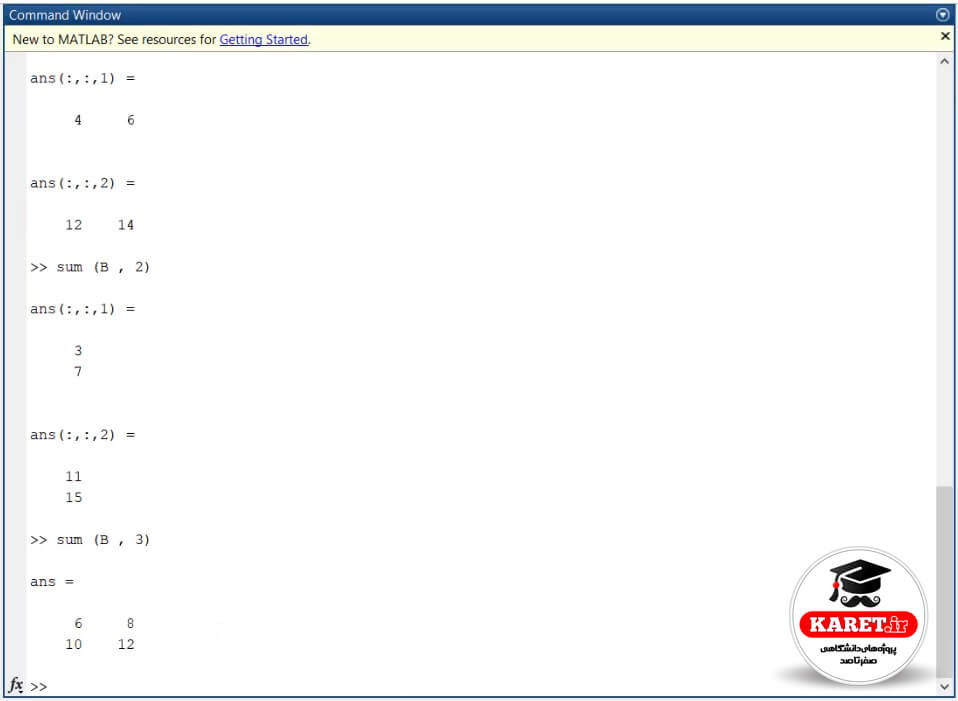
یعنی اینکه همهی طبقات (هر سه طبقه) با هم جمع شده است. چگونه؟
ماتریسهای ما در بعد اول و بعد دوم به ترتیب به صورت زیر بودند.
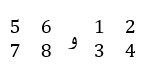
6 = 5 +1 و 10 = 7 + 3 ، 8 = 6 + 2 و 12 = 8 + 4 که جواب نهایی به صورت زیر به دست آمده است.

حال میتوانیم ماتریس B را به گونهی دیگری تعریف کنیم و بگوییم که بعد سوم هم دارد. میگوییم همهی سطرها و همهی ستونها در بعد سوم میشود: [12 11 ; 10 9]
این یک ماتریس سهبعدی شده است و اگر جواب را مشاهده کنید، خواهید دید که B به صورت ماتریس سه بُعدی 3 × 2 × 2 است. حال اگر به صورت (:)B بنویسیم که آن را به بردار تبدیل کنیم، به صورت زیر خواهد شد.
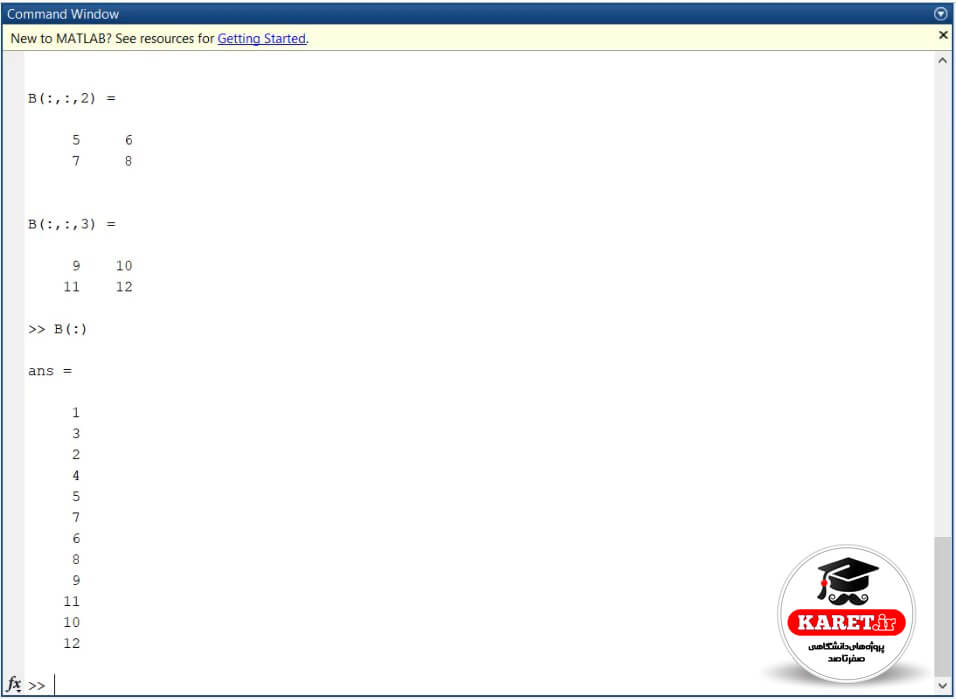
همانطور که قبلا در عکس برایتان توضیح دادم، ابتدا ستون اول و بعد ستون دوم و ستون سوم سپس ستون سوم و تا آخر ادامه میدهیم و اگر بخواهیم جمع آنها را به دست آوریم، مینویسیم sum (C(:)) یعنی sum (C) همهی آن.
در اینجا C را اشتباه نوشتیم زیرا در واقع ماتریس B را داشتیم.
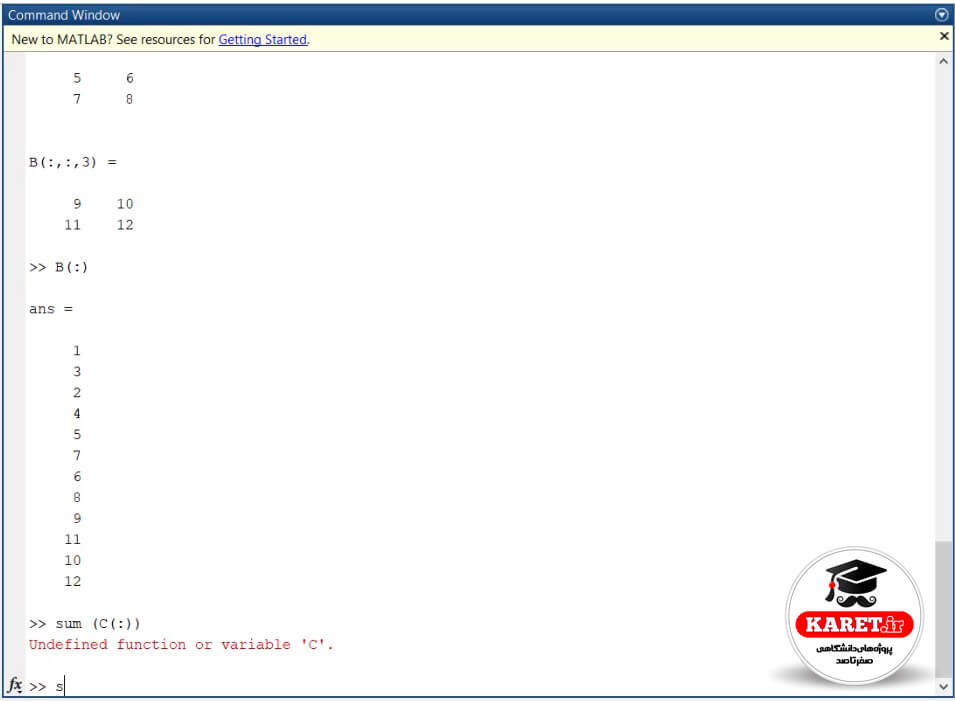
بنابراین به صورت sum (B(:)) مینویسیم که مشاهده میکنیم که در جواب ۷۸ را به ما میدهد.
در صورتی که شما پس از خواندن محتوای جلسات قبلی و این بخش که به سادهترین زبان ممکن دربارهی برنامهی متلب و محیط کاربری آن توضیح داده باز هم سردرگم هستید. میتوانید با برون سپاری انجام پروژه متلب خود به کارشناسان حرفهای کارت پروژه میباشد. میتوانید از طریق شمارهی 09104503300 با پشتیبانان کارت از طریق پیام یا تماس در ارتباط باشید.
در جلسه آینده با تغییر شکل یک ماتریس در متلب آشنا خواهیم شد.
برای کسب اطلاعات بیشتر در مورد متلب میتوانید به مقاله آموزش متلب مقدماتی مراجعه کنید.











ارسال پاسخ