در این دوره آنلاین آموزش متلب به صورت رایگان با سری آموزشهای نرم افزار متلب در خدمت شما هستیم. جلسه گذشته در رابطه دستور reshape در متلب (تغییر شکل ماتریس در متلب) صحبت کردیم. در این جلسه آموزشی قصد داریم به مبحث کاربرد دستور diag در متلب بپردازیم. در واقع آنچه که شما به طور کاملا عملی برای استفاده در انجام پروژه متلب نیاز دارید در این جلسات ارائه خواهد شد.
کاربرد دستور diag در متلب
دستور diag را داریم. این دستور عناصر قطری را به ما میدهد. در اصل دو تا کار انجام میدهد. این دستور دو کار انجام میدهد. یکی از کارها این است که این دستور عناصر قطر اصلی را به صورتی که در تصویر زیر مشاهده میکنید به ما میدهد.
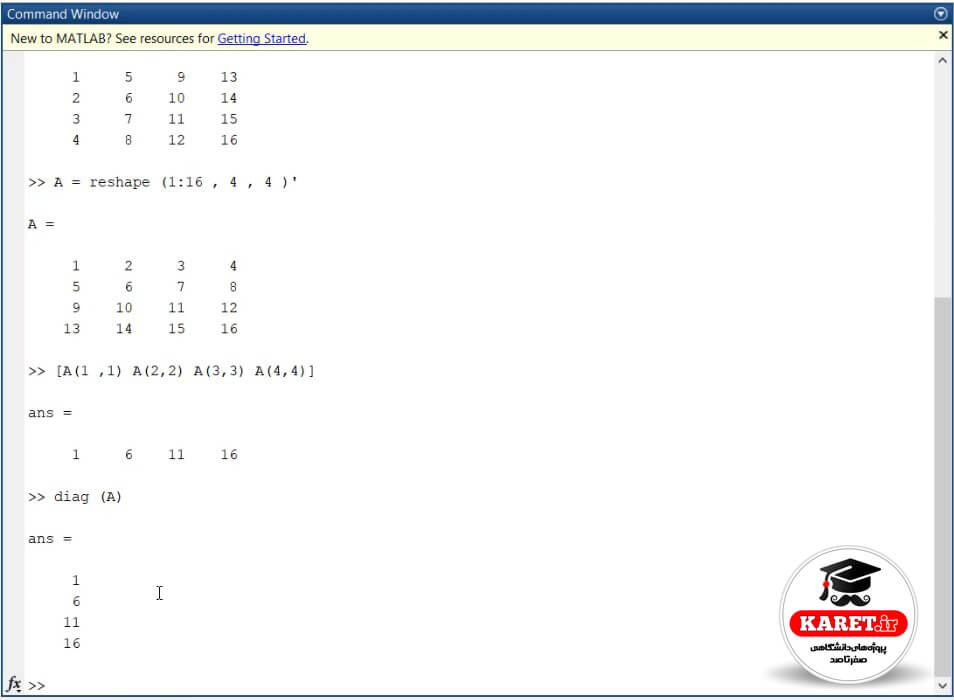
اما همیشه که قطر ما به این صورت نیست. به طور مثال ماتریس ما ۴×۴ یا ۲×۲ یا ۶×۶ نیست. گاهی اوقات ممکن است ماتریسی مانند B به صورت زیر داشته باشیم.
B = reshape (1: 12 , 3 , 4)t
که transpose هم شده است.
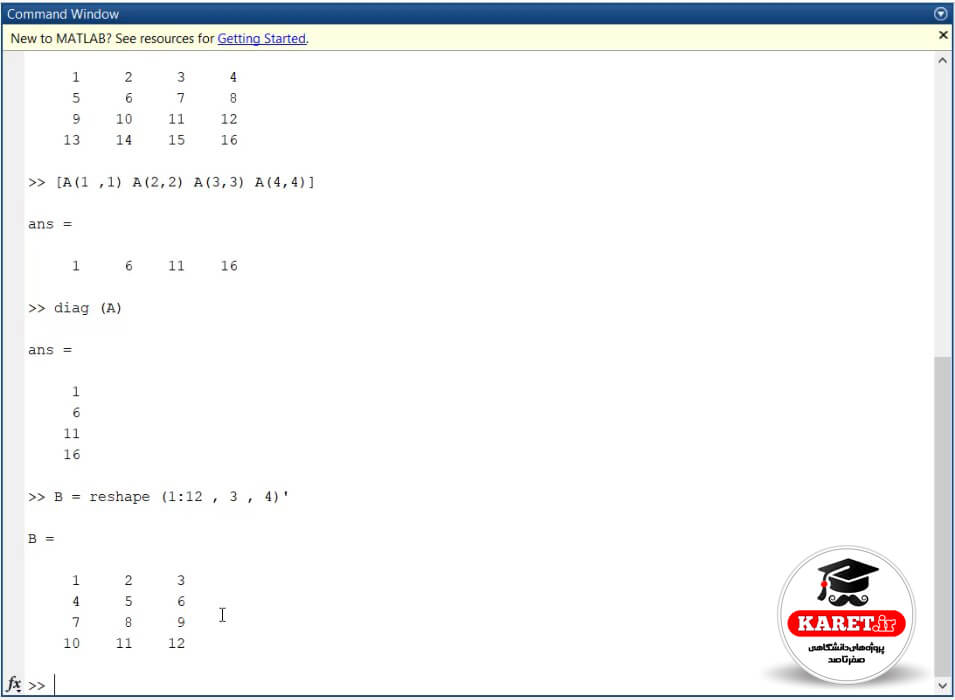
مشاهده میکنید که یک ماتریس دارای ۴ سطر و ۳ ستون است. به نظر شما وقتی diag این ماتریس را بگیریم، قطر اصلی آن چه خواهد بود؟ به صورت زیر مینویسیم تا قطر اصلی آن را به ما بدهد.
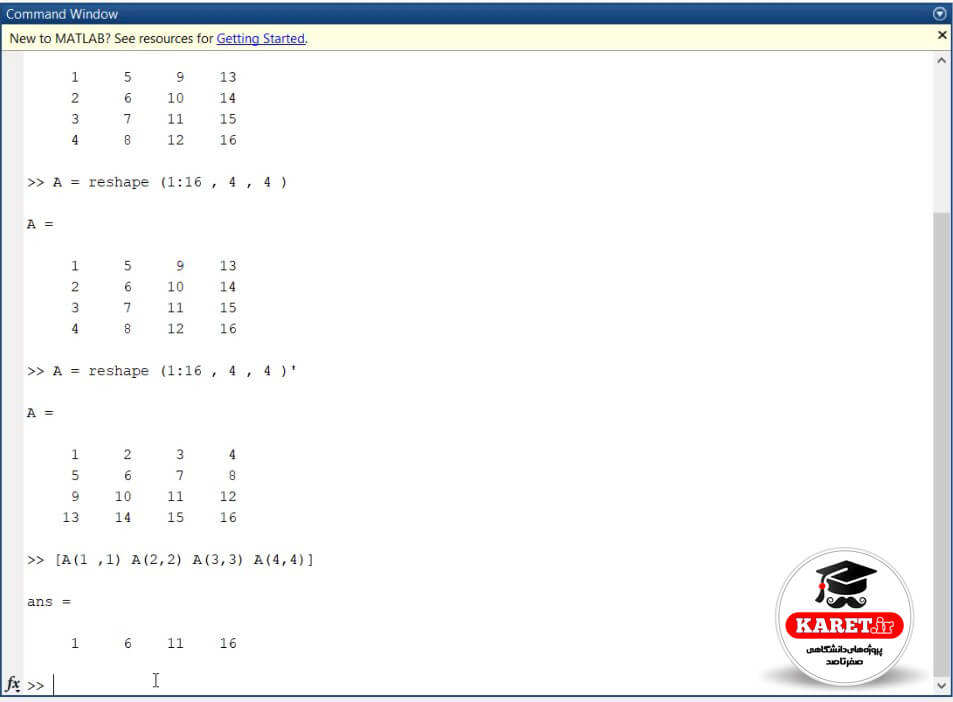
مشاهده میکنیم که جواب را به ما داده است. از اینجا نتیجه میگیریم که diag مینیمم سطر و ستون را برای به دست آوردن قطر در نظر میگیرد. حال به نظر شما diag( [1 3 6] ) چیست؟ آیا جواب ۱ است؟ شما چه فکری میکنید؟
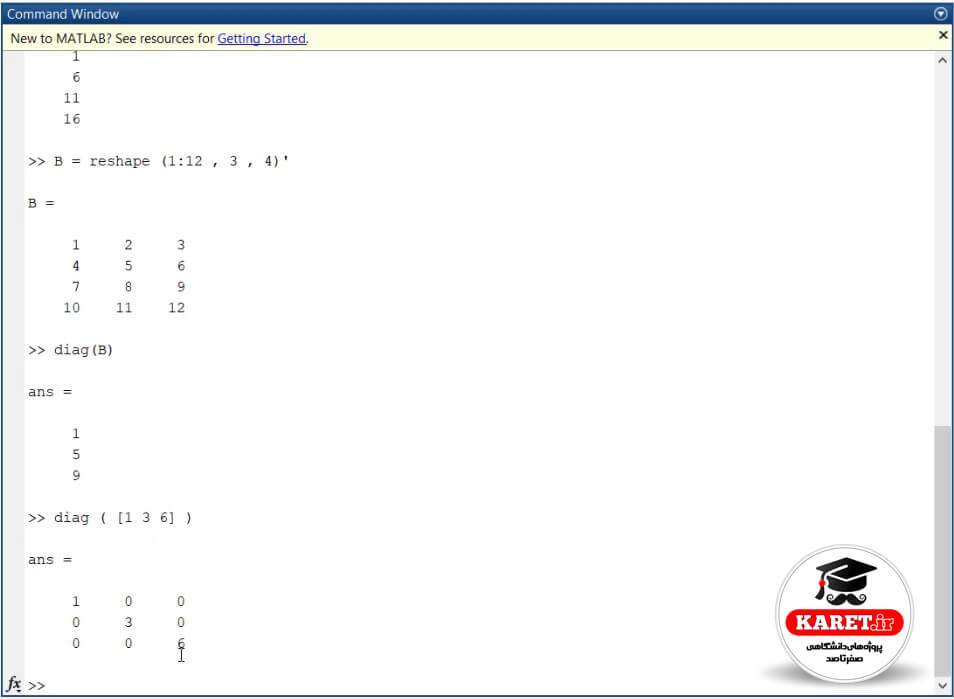
در اینجا اگر مشاهده کنید، دیگر ۲ را به ما نمیدهد. به ما یک ماتریس داده است که اعضای قطر اصلی آن ۱ و ۳ و ۶ است.
این یعنی اینکه برای دستور diag وقتی که ما به آن یک بردار یا بهتر است بگوییم قطر بدهیم، به ما یک ماتریس را میدهد که عناصر غیر از قطر اصلی آن صفر است و با صفر متقارن هم است و اگر ماتریس را به آن بدهیم، به ما قطر آن ماتریس را میدهد.
بنابراین دستور diag در اصل دو حالت دارد؛ به طور مثال فرض کنید که diag (A) را که در بالا محاسبه کرده بودیم، این بار به صورت زیر مینویسیم و میخواهیم diag (diag (A) ) را به دست آوریم.
به نظر شما جواب چه میشود؟ کمی روی آن فکر کنید.
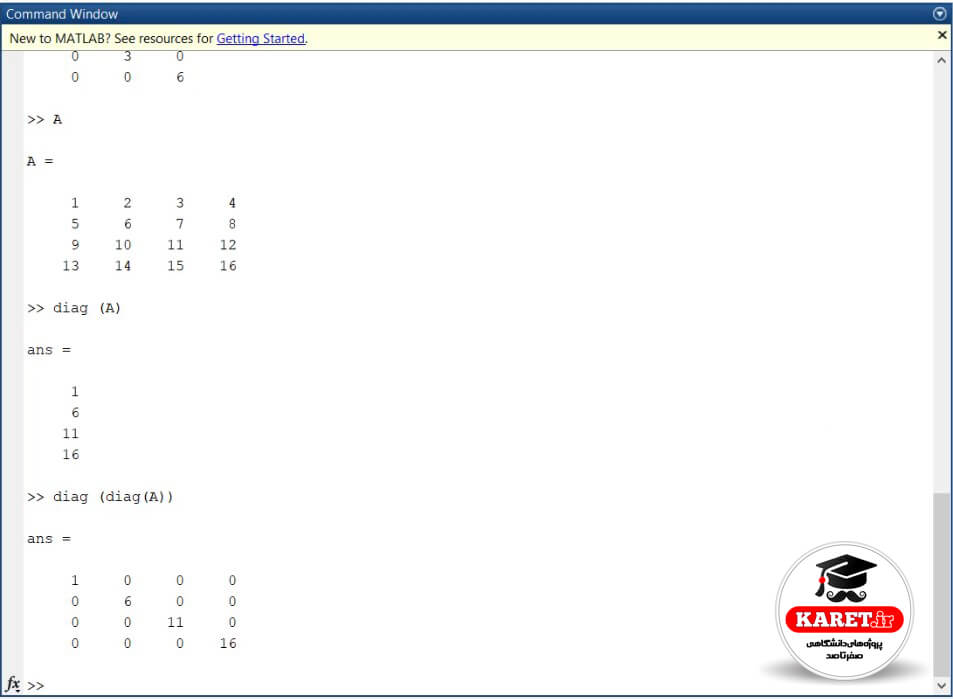
مشاهده میکنید که ماتریسی را به ما داده است که قطر اصلی ماتریس A را گرفته است و بقیه عناصر را صفر کرده است.
حال یک تمرین به شما میدهم تا کمی روی آن فکر کنید. فرض کنید که ماتریس A را به ما دادند و میگویند که عناصر قطر اصلی را یا صفر کنید یا دو برابر کنید. چگونه باید این کار را انجام دهیم؟ کمی روی جواب این سؤال فکر کنید.
کار سادهای است. میگوییم که خود ماتریس A منهای diag (diag (A) ) که حاصل آن به ما ماتریسی میدهد که قطرهای آن صفر است. در واقع همان ماتریس A است که عناصر واقع در قطر اصلی آن صفر شده است. زیرا عناصر قطر اصلی در ماتریس diag (diag (A) ) از آن کم شده است.
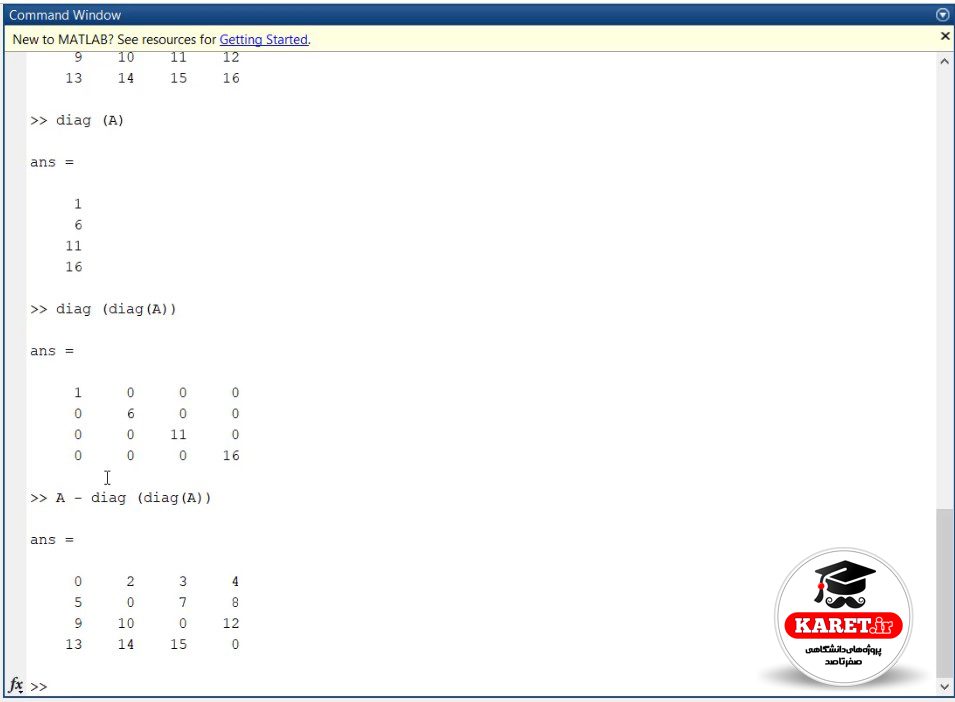
حال اگر بخواهیم آن را دو برابر کنیم، چه کاری انجام میدهیم، همان فرمول بالا ولی به جای علامت منها (-)، از علامت به اضافه (+) استفاده میکنیم.
A + diag (diag (A) )
حال فرض کنید که ما بخواهیم یک ماتریس تصادفی را تعریف کنیم. ماتریس تصادفی یک ویژگیهایی دارد که در اینجا به آن اشاره میکنم. به طور مثال اگر بخواهیم ماتریس A را به صورت تصادفی تعریف کنیم، این ماتریس باید مثبت باشد، یعنی باشد.
دومین ویژگی این است که یعنی ماتریس باید متقارن باشد. ماتریس متقارن چیست؟ ماتریس متقارن یعنی symmetric matrix. یعنی اینکه ماتریسی است که درایههای آن نسبت به قطر اصلی آن دقیقاً یکسان است و نسبت به هم متقارن هستند. این تعریف ماتریس متقارن میشود.
که اگر بخواهیم آن را در متلب هم به دست آوریم، میشود (A+A’)/2 که A’ همان transpose ماتریس A است.
در این صورت ما میتوانیم یک ماتریس متقارن داشته باشیم.
سومین ویژگی به ما میگوید که یعنی مساوی صفر باشند یعنی قطر اصلی آن در ماتریس تصادفی صفر باشد و آخرین ویژگی یعنی به ما میگوید که آن جزو اعداد صحیح باشد و تعریف اعداد صحیح هم همین را میگوید که اگر ریاضیات را به خاطر بیاورید، تعریف اعداد صحیح به این صورت است.
حال ما میخواهیم این را در متلب اجرا کنیم و ماتریس تصادفی بسازیم. ابتدا clear میکنیم که workspaceمان خالی شود. سپس میخواهیم بگوییم که یک ماتریس A را به صورت تصادفی به ما بدهد. بنابراین randi را تایپ میکنیم و برای مثال میگوییم که از ۴۰ تا ۱۲۰ باشد و اینکه ۶ تا سطر و ۶ تا هم ستون داشته باشد.
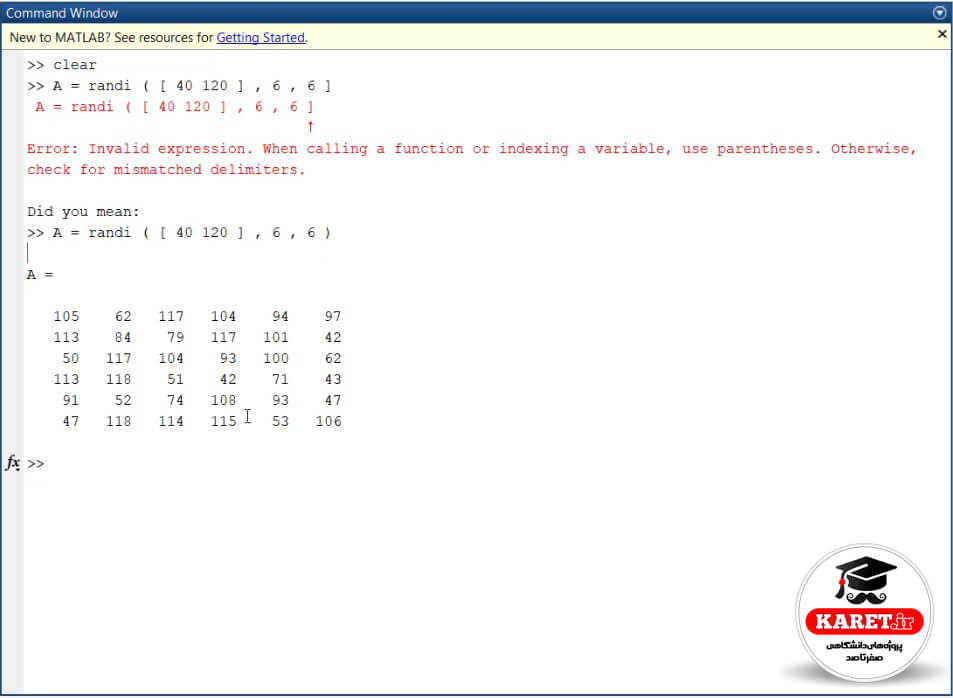
یک ماتریس رندوم به ما میدهد که اعضای آن از ۴۰ تا ۱۲۰ باشند و دارای ۶ سطر و ۶ تا ستون باشد.
مشاهده میکنید که ماتریس حاصل ۶ سطر و ۶ ستون دارد و اعداد آن هم به صورت تصادفی داده شدهاند.
حال اگر بخواهیم آن را متقارن کنیم، چگونه آن را متقارن میکنیم؟ به صورت زیر مینویسیم:
A = (A+A’)/2
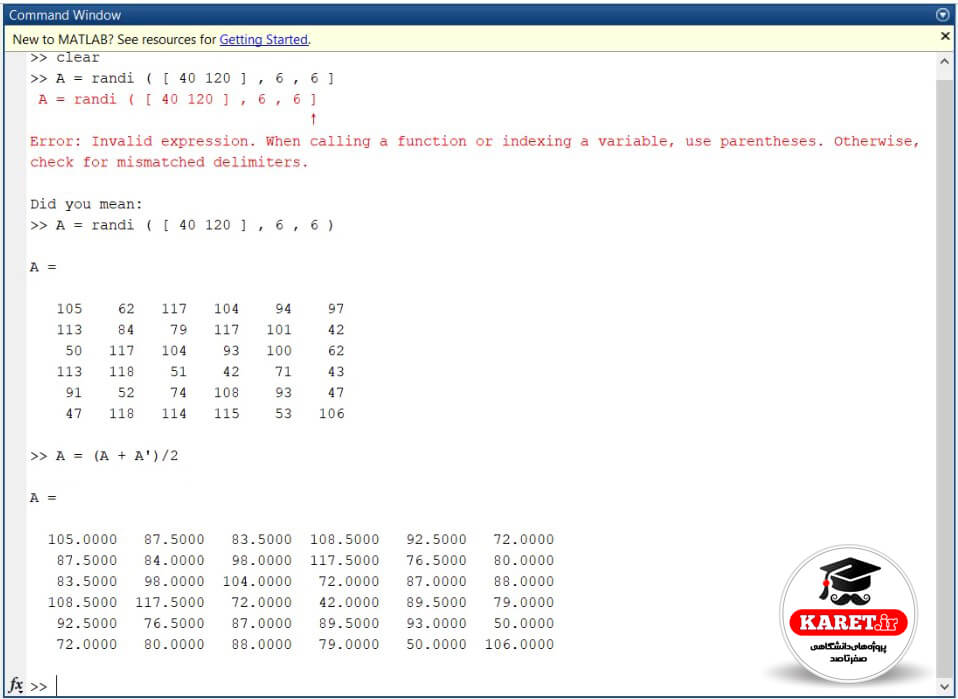
همانطور که مشاهده میکنید، ماتریس حاصل به صورت متقارن درآمده است. یعنی نسبت به قطر اصلی متقارن است.
حال میخواهیم اعضای آن به صورت عدد صحیح باشند یعنی به طور مثال در اینجا نیم نداشته باشیم. چگونه باید به دست آوریم؟
برای اینکه A را جزء اعداد صحیح کنیم، به صورت زیر مینویسیم:
A = floor ( (A+A’)/2 )
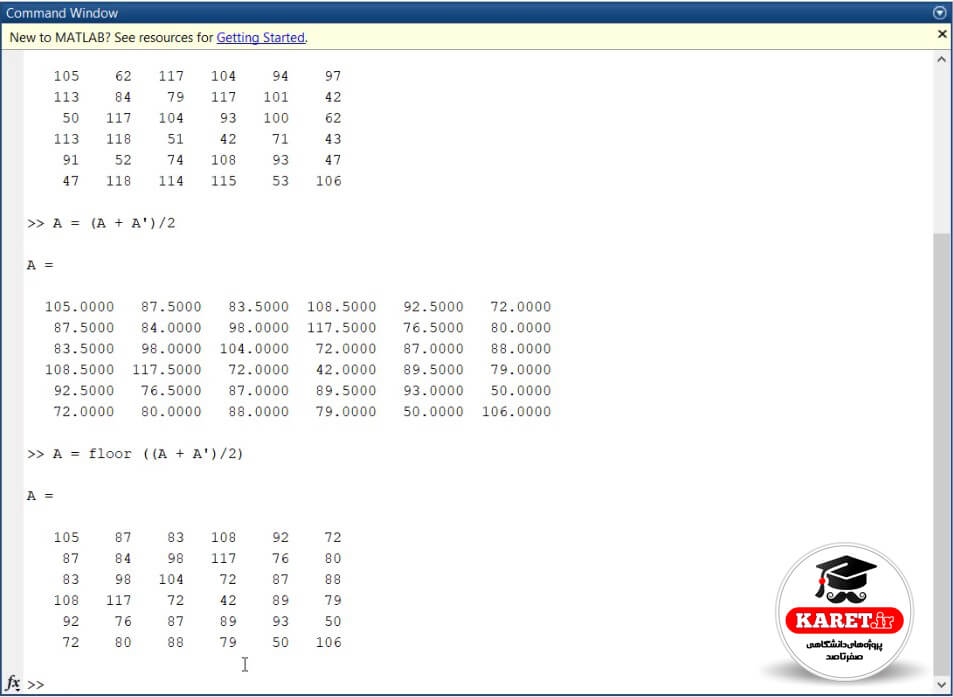
که همانطور که در تصویر بالا مشاهده میکنید، پاسخ به صورت عدد صحیح درمیآید.
و در آخر میخواستیم که قطر اصلی آن نیز صفر کنیم که راه حل این سؤال را هم در بالاتر گفته بودیم و به صورت زیر خواهد بود:
A = A – diag (diag (A) )
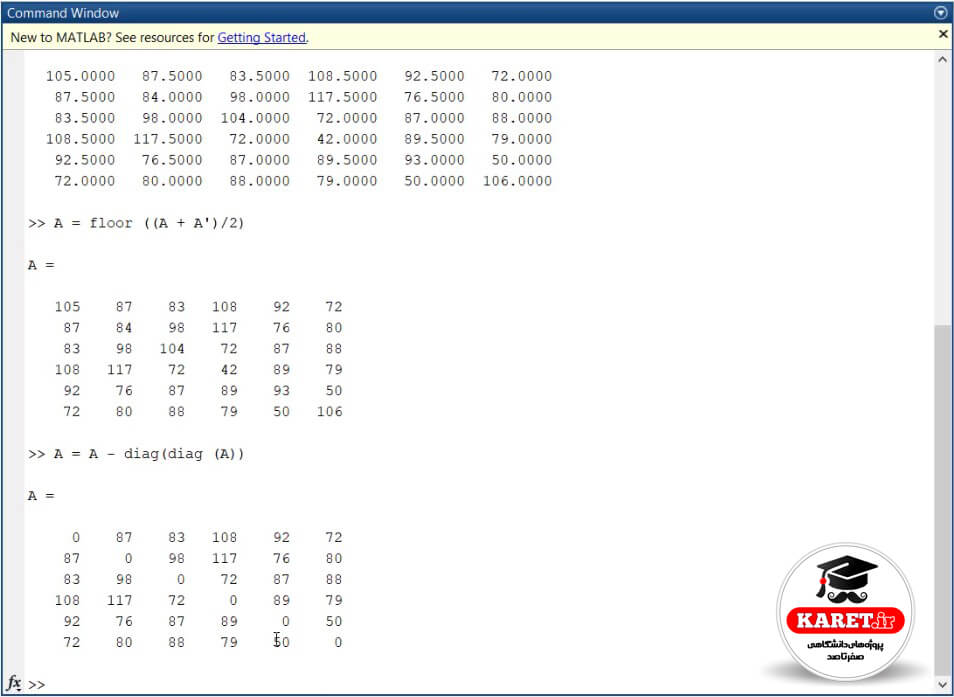
و مشاهده میکنید که به راحتی قطر اصلی A صفر شده است.
در جلسه آینده با گرد کردن (رند کردن) اعداد در متلب با دستور round، ceil و floor آشنا خواهیم شد.
در صورتی که شما پس از خواندن محتوای جلسات قبلی و این بخش که به سادهترین زبان ممکن دربارهی برنامهی متلب و محیط کاربری آن توضیح داده باز هم سردرگم هستید. میتوانید با برون سپاری انجام پروژه متلب خود به کارشناسان حرفهای کارت پروژه میباشد. میتوانید از طریق شمارهی 09104503300 با پشتیبانان کارت از طریق پیام یا تماس در ارتباط باشید.
برای کسب اطلاعات بیشتر در مورد متلب میتوانید به مقاله آموزش متلب مقدماتی مراجعه کنید.











ارسال پاسخ