اما از اینجا به بعد میخواهیم یک مثال مهم را در این آموزش از متلب بیان کنیم.
حل مثالی با استفاده از تابع norm در متلب
ابتدا یک فرمول را معرفی میکنیم.
l=√(|x_1 |^p+|x_2 |^p+⋯+|x_n |^p )
در فرمول فوق تعداد ورودیها و خروجیها را مشخص کنید. کمی فکر کنید و بگویید که کدام ورودی و کدام خروجی است. و اینکه بگویید چند تا متغیر داریم. روی همه این سؤالات فکر کنید و جواب آن را بگویید.
در اینجا خروجی ما l است. همانطور که میبینید l برابر این فرمول شده است و ورودیهای ما p و x ها هستند. ولی در اینجا تعداد xها نامحدود است و اگر بخواهیم این را به صورت یک تابع تعریف کنیم، برای xها باید از varargin استفاده کنیم. یک p هم داریم. به نظر شما p چیست؟ p هم از جنس ورودی است. پس ما دو نوع ورودی داریم؛ یکی xها که برای argin استفاده میکنیم و یکی p.
اگر به انجام پروژه متلب علاقمند هستید می توانید با کارشناسان ما جهت ثبت سفارش در ارتباط باشید.
حال میخواهیم این فرمول را اجرا کنیم.
میخواهیم به صورت عملی در یک function این فرمول را اجرا کنیم.
ابتدا باید یک تابع دیگر در اینجا به نام norm تعریف کنیم.
نام تابع را Norm قرار میدهیم.
یک function داریم که خروجی آن l بود. در اینجا L میگذاریم. نام آن را Norm گذاشتیم. برای ورودی یک varargin و p داشتیم.
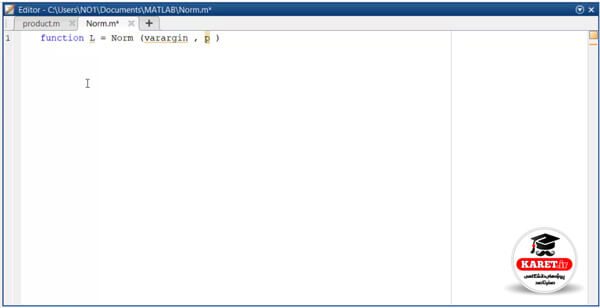
به نظر شما این نوع نوشتن درست است یا خیر، باید p را در ابتدا قرار دهیم؟
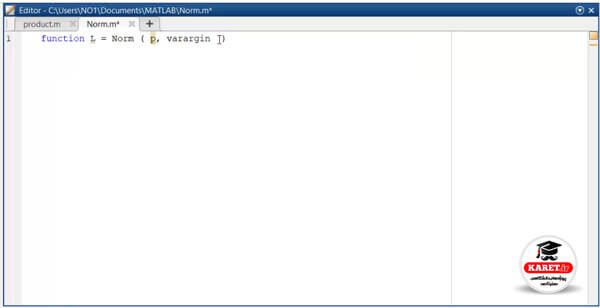
به نظر شما کدام درست است؟
برنامه نوشته شده در تصویر دوم درست است و نباید p را آخر قرار دهیم. زیرا varargin تعداد بینهایت است و مشخص نیست چه زمانی تمام شود. اگر ما varargin را ابتدا قرار دهیم و بعد p را قرار دهیم (p یک تعداد معلومی است)، نمیداند varargin چه زمانی تمام میشود و به همین دلیل میبینید که اشتباه است و باید به این صورت بنویسیم که varargin همیشه آخر باشد.
همیشه هرچند تا که ورودی داشتید، varargin را باید در آخر قرار دهید.
باید اعضای داخل varargin را داخل یک بردار بریزیم. زیرا آرایههای سلولی هستند.
فرض کنید ما H را داریم. اعضای آن هم ۲ و ۳ و ۷ و۵ هستند. این H سلولی است.
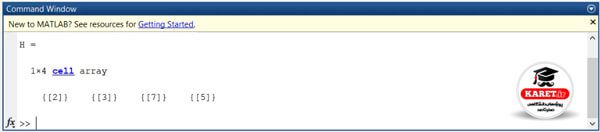
اگر بخواهید اینها را به ماتریس تبدیل کنید، باید بگوییم که x=cell2mat(H) یعنی سلول را به ماتریس H تبدیل کند.
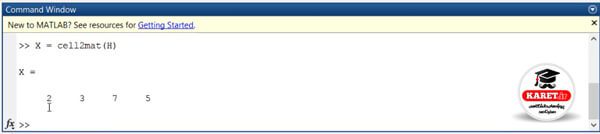
الان آن را به صورت یک بردار درآورد و آن را ماتریسی کرد. پس این حرکت را باید برای این function انجام دهیم.
ابتدا باید بگوییم که x=cell2mat(varargin) زیرا اعضای varargin را میخواستیم. بعد از آن باید فرمولمان را بنویسیم.
قدرمطلق x را داشتیم که با abs(x) نشان میدهیم. به توان p میرسانیم. ولی باید همه xها را با هم جمع میکردیم. پس باید یک sum هم در ابتدای فرمول قرار دهیم و بقیه را داخل پرانتز قرار دهیم.
Sum xها یک جذر هم داشت یعنی به توان مانند۱/۲ و ۱/۳و … پس جذر آن میشود به توان 1 تقسیم بر p

چرا به توان شد؟ مثلا خالی بدون فرجه را در نظر بگیرید. P آن برابر ۲ است. رادیکال یعنی به توان
پس در اینجا میشود ۱ تقسیم بر p
حال end را میزنیم و تمام میشود.
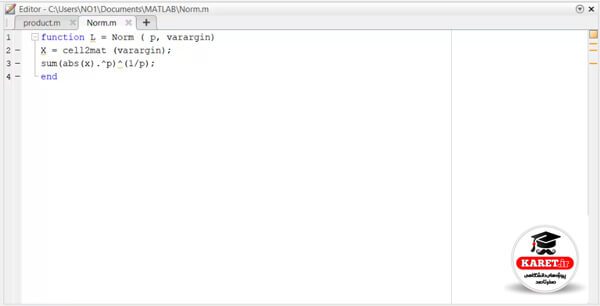
برای مثال میخواهیم Norm(2,3,4) را محاسبه کنیم. یعنی رادیکال با p=2 باشد.
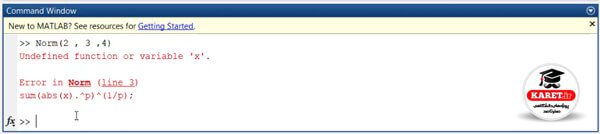
در خط دوم x را با حروف بزرگ نوشتیم که باید با حروف کوچک باشد.
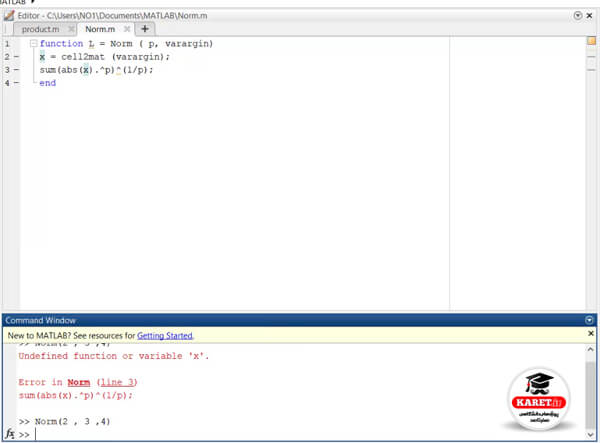
و همچنین توجه کنید که در خط سوم هم باید L = را قبل از sum قرار میدادیم
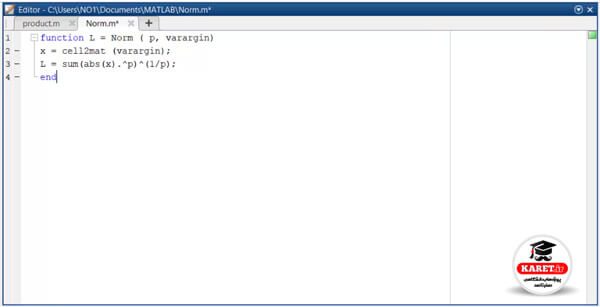
الان برنامه درست نوشته شده است و مربع با رنگ سبز نشان میدهد که هیچ مشکلی در برنامه وجود ندارد.
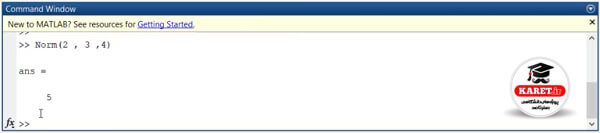
چرا جواب ۵ شده است؟
جواب به سادگی با فرمول فوق محاسبه شده است.
برای مثال فرض کنید که همین فرمول را برای p=1 در نظر بگیرید.
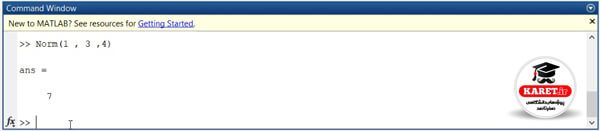
جواب ۷ است.
برای مثال p را برابر ۱۰۰ در نظر میگیریم. در این صورت اگر از ریاضیات به یاد داشته باشید، بزرگترین را در نظر میگرفت. در اینجا باید به ما جواب ۴ را بدهد.
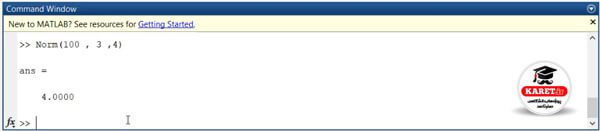
هر وقت عدد p خیلی بزرگ شد، بزرگترین عدد متغیر را میدهد.
در مثال زیر جواب باید ۷ باشد که مشاهده میکنید همینطور است.
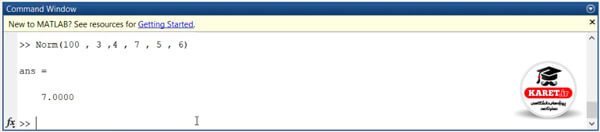
حال با موضوع cell2mat که یاد گرفتید، اگر بخواهید تابع قبلی را به گونهی دیگری بنویسیم که راحتتر باشد، چگونه میتوانیم آن را بنویسیم؟ میتوانیم بنویسیم x=cell2mat(varargin) و در خط بعدی بنویسیم p=prod(x)
بعد از آن هم یک end داریم.
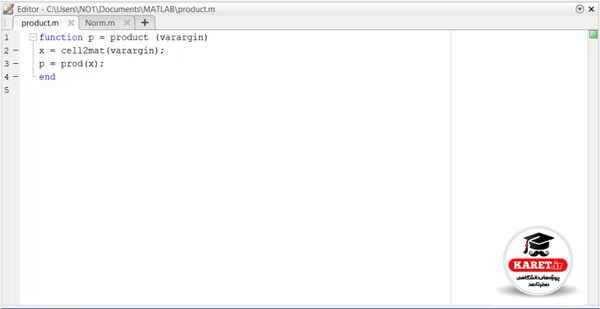
برای مثال product(1,2,3) را میخواهیم.
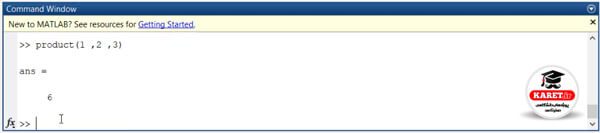
مشاهده میکنید که دقیقا همان جواب را به ما میدهد و هیچ تفاوتی با قبلی ندارد. ولی در کد قبلی که نوشتیم، اگر ورودیها چند تا ماتریس باشد، [۱۷:۳۱] ؟؟؟ که در اینجا نمیتوان استفاده کرد و در اینجا جواب نمیدهد و باید دقت کنید که وقتی دارید کدنویسی میکنید باید بدانید چه چیزی میخواهید تا کدهایتان را بسیار بهتر بنویسید.
تا جلسهی آینده شما را به خدای مهربان میسپارم.










ارسال پاسخ