در دنیای ریاضیات، بزرگترین مقسومعلیه مشترک (ب.م.م) به عنوان بزرگترین عددی که میتواند دو یا چند عدد را بدون باقیمانده تقسیم کند، نقش اساسی در محاسبات دارد. این مفهوم، یکی از مفاهیم پایه برای درک ساختار اعداد و روابط آنهاست.
در برنامهنویسی هم، محاسبه ب.م.م به بهینهسازی الگوریتمها و حل مسائل متنوع کمک میکند. برای مثال، در رمزنگاری، ب.م.م در الگوریتمهای کلید عمومی یا public مانند RSA برای تولید کلیدها استفاده میشود؛ یا در سیستمهای مدیریت داده، برای سادهسازی کسرها و بهینهسازی محاسبات با ب.م.م سر و کار دارند.
در زبان برنامهنویسی پایتون که موضوع ما در این مطلب است، ابزارها و توابع متعددی برای محاسبه ب.م.م وجود دارد که هرکدام از آنها میتوانند این مفهوم ریاضی را به صورت کارآمد در برنامهها پیاده کنند. در این مقاله از سایت انجام پروژه های دانشجویی کارت پروژه با ما همراه باشید تا موارد زیر را با هم آموزش ببینیم:
- 2 روش محاسبه ب.م.م در پایتون
- کاربردهای ب.م.م در پایتون
- چالشهای رایج در محاسبه ب.م.م در پایتون و روشهای مقابله با آنها
روشهای محاسبه ب.م.م در پایتون
در پایتون، برای محاسبه بزرگترین مقسومعلیه مشترک (ب.م.م) دو عدد، از دو روش اصلی میتوان استفاده کرد:
1. استفاده از تابع داخلی gcd در ماژول math
پایتون از نسخه 3.5 به بعد، تابعی به نام gcd در ماژول math ارائه داد که این تابع محاسبه ب.م.م در پایتون را بسیار ساده میکند.
برای استفاده از این تابع، ابتدا باید ماژول math را وارد کنید:
import math
سپس میتوانید ب.م.م دو عدد را به صورت زیر محاسبه کنید:
x = 48
y = 18
result = math.gcd(x, y)
print(result) خروجی: 6 #
در این مثال، تابع math.gcd ب.م.م اعداد 48 و 18 را محاسبه کرده و نتیجه 6 را حاصل میکند.
خدمت پیشنهادی مرتبط: انجام پروژه پایتون
2. پیادهسازی الگوریتم اقلیدسی
شاید اسم الگوریتم اقلیدسی (Euclidean Algorithm) را شنیده باشید. این الگوریتم یکی از قدیمیترین و کارآمدترین روشها برای محاسبه ب.م.م است و بر اساس تقسیم متوالی اعداد و استفاده از باقیماندهها ب.م.م را به دست میآورد.
مراحل اجرای الگوریتم اقلیدسی برای محاسبه ب.م.م به صورت زیر است:
- عدد بزرگتر را بر عدد کوچکتر تقسیم کنید.
- اگر باقیمانده صفر است، عدد کوچکتر ب.م.م است.
- در غیر این صورت، عدد کوچکتر را جایگزین عدد بزرگتر کرده و باقیمانده را جایگزین عدد کوچکتر کنید.
- این فرآیند را تکرار کنید تا باقیمانده صفر شود.
پیادهسازی این الگوریتم برای محاسبه ب.م.م در پایتون به صورت بازگشتی و اینچنین است:
:def gcd(a, b)
:if b == 0
return a
:else
return gcd(b, a % b)
result = gcd(48, 18)
خروجی: 6 # print(result)
در هر دو روش پیادهسازی، ب.م.م اعداد 48 و 18 برابر با 6 است.
استفاده از تابع داخلی gcd در ماژول math شاید روش سادهتر و خواناتری برای شما به نظر برسد، اما یادگیری و پیادهسازی الگوریتم اقلیدسی هم در نوع خود میتواند شما را به درک عمیقتری از نحوه محاسبه ب.م.م برساند و در مواردی کارآمد باشد.
حال که به دنبال آموزش ب.م.م در پایتون هستید، جالب است بدانید مجموعه ما در حوزه های مختلف کاربرد پایتون خدمات ارائه میدهد. در زیر برخی از این خدمات را آوردهایم:
انجام پروژه برنامه نویسی | انجام پروژه ماشین لرنینگ | انجام پروژه هوش مصنوعی
انجام پروژه شبکه عصبی | انجام پروژه داده کاوی | انجام پروژه پردازش تصویر
کاربردهای ب.م.م در پایتون
در برنامهنویسی، مفهوم ب م م یا همان بزرگترین مقسومعلیه مشترک نقش مهمی در بهینهسازی و سادهسازی محاسبات ایفا میکند. دو کاربرد اصلی ب.م.م در برنامهنویسی از این قرارند:
سادهسازی کسرها
یکی از کاربردهای رایج ب.م.م در برنامهنویسی، سادهسازی کسرها است. به عبارت دیگر، با تقسیم صورت و مخرج یک کسر بر ب.م.م آنها، میتوان کسر را به سادهترین شکل ممکن درآورد. این کار در بسیاری از برنامهها، بهویژه در محاسبات ریاضی و گرافیکی، ضروری است.
مثال:
فرض کنید کسر 12/8 را داریم. ب.م.م اعداد ۸ و ۱۲ برابر با ۴ است و با تقسیم صورت و مخرج بر ۴، کسر به 3/2 تبدیل میشود.
در پایتون اینگونه عمل میکنیم:
import math
:def simplify_fraction(numerator, denominator)
gcd = math.gcd(numerator, denominator)
return numerator // gcd, denominator // gcd
استفاده از تابع #
numerator, denominator = 8, 12
simplified_numerator, simplified_denominator = simplify_fraction(numerator, denominator)
(“{simplified_numerator}/{simplified_denominator} :کسر سادهشده “print( f
خروجی:
کسر سادهشده: 3/2
پیش از ادامه مقاله، شاید برایتان مفید باشد بدانید مقاله های زیر میتوانند اطلاعات بیشتری در زمینه پایتون در اختیار شما قرار دهند:
- ک م م در پایتون (به 4 روش مختلف)
- حلقه for در پایتون + نحوه استفاده و مثال کاربردی
- حلقه while در پایتون (توضیح ساده به همراه مثال تصویری)
- دستورات شرطی در پایتون (آموزش ساده به همراه تصاویر)
2. تعیین نسبتهای مشترک
در بسیاری از مسائل برنامهنویسی، نیاز داریم نسبتهای مشترک بین اعداد مختلف را تعیین کنیم. ب.م.م میتواند در این زمینه کمککننده باشد. برای مثال، در الگوریتمهای گرافیکی یا فیزیکی، ممکن است بخواهیم نسبتهای مشترک بین ابعاد مختلف را پیدا کرده و از آن استفاده کنیم.
مثال:
فرض کنید دو مستطیل با ابعاد 12*8 و 15*10 داریم. برای یافتن نسبتهای مشترک، میتوانیم ب.م.م ابعاد را محاسبه کرده و سپس نسبتها را تعیین کنیم.
برای محاسبه ب.م.م در پایتون چنین عمل میکنیم:
import math
:def find_common_ratio(dim1, dim2)
gcd = math.gcd(dim1, dim2)
return dim1 // gcd, dim2 // gcd
استفاده از تابع #
width1, height1 = 8, 12
width2, height2 = 10, 15
width_ratio, height_ratio = find_common_ratio(width1, width2)
(“1: {width_ratio}:نسبت عرضها”f) print
(“1: {height_ratio}:نسبت ارتفاعها”f)print
خروجی:
نسبت عرضها: 4:5
نسبت ارتفاعها: 4:5
در این مثال، با استفاده از مفهوم ب.م.م، توانستیم نسبتهای مشترک بین ابعاد دو مستطیل را پیدا کنیم. این یک مثال کاربردی بود که نشان میداد ب.م.م در برنامهنویسی ابزار مهم و قدرتمندی است که میتواند در بهینهسازی محاسبات و سادهسازی مسائل ریاضی کمککننده باشد.
معمولا کسانی که به دنبال یادگیری پایتون هستند، دانشجوی رشتههای مهندسی هستند. خبر خوب این است که ما در کارت پروژه خدمات مربوط به تمامی رشتهها از جمله رشته های مهندسی زیر را ارائه میکنیم:
چالشهای رایج در محاسبه ب.م.م در پایتون و روشهای مقابله با آنها
محاسبه ب.م.م در پایتون همیشه هم به این سادگی نیست. گاهی ممکن است با مشکلاتی در فرآیند به دست آوردن ب م م مواجه شوید و کدهای پایتون شما را به چالشهایی بکشند که نیاز به بررسی و رفع آنها دارید. آشنایی با این چالشها هم برای افراد مبتدی مفید است، هم به حرفهایها کمک میکند تا در پروژههای برنامهنویسی و محاسبات ب.م.م کمتر با مشکل روبرو شوند.
مهمترین این چالشها و روشهای مقابله با آنها در اینجا آمده:
عملکرد ضعیف در اعداد بزرگ
در محاسبات ب.م.م در پایتون با استفاده از الگوریتمهای سنتی، در صورتی که با اعداد بزرگ سر و کار داشته باشید، ممکن است سرعت محاسبه به اندازه انتظارتان بالا نباشد. برای مقابله با این مشکل، از الگوریتمهای بهینهتری مانند الگوریتم اقلیدسی بهینهسازی شده استفاده کنید که زمان اجرای آن کمتر است.
استفاده از نسخههای بهینهشده الگوریتمها یا استفاده از کتابخانههایی که مخصوص محاسبات و کار کردن با اعداد ماتریسهای بزرگ طراحی شدهاند، مانند numpy یا sympy راهکار خوبی در این مواقع است.
خطاهای ناشی از نوع دادهها
در مواقعی که با نوع خاصی از دادهها (مانند اعداد صحیح و اعشاری) کار میکنید، شاید گرفتن ب.م.م در پایتون به مشکل بربخورد. مثلا، استفاده از اعداد اعشاری به جای اعداد صحیح میتواند به نتایج نادرست منتهی شود.
راهکار این مشل این است که اول اطمینان حاصل کنید که ورودیهای تابع ب.م.م از نوع داده صحیح (int) باشند. در صورتی که اینطور نیست، آنها را به اعداد صحیح تبدیل کنید.
محاسبه ب.م.م اعداد منفی
محاسبه ب.م.م در اعداد منفی هم چالشبرانگیز است، زیرا در بسیاری مواقع الگوریتمهای سنتی محاسبه ب.م.م در پایتون جواب نادرستی ارائه میدهند. برای مقابله با این مشکل، هروقت با ورودیهای منفی روبرو شدید، قبل از محاسبه ب.م.م، تمام آنها را به مقادیر مثبت تبدیل کنید. دلیل اصلی این کار این است که در اکثر زبانها و کتابخانهها، ب.م.م همیشه عددی مثبت تعریف میشود.
تفاوتهای پیادهسازی در زبانهای مختلف
در بعضی از زبانهای برنامهنویسی، روشهای پیادهسازی مختلفی برای محاسبه ب.م.م وجود دارد که همین موضوع شاید منجر به تفاوت در نتایج به دست آمده شود. بیشتر وقتها زمانی متوجه این مسئله میوید که در پروژههای چندزبانه کار میکنید.
راه حل این است که برای پروژههایی که قرار است در چند زبان برنامهنویسی مختلف آنها را پیادهسازی کنید، از روش پیادهسازیهای استاندارد و پذیرفتهشدهای مانند الگوریتم اقلیدسی استفاده کنید تا مطمئن شوید که نتایج یکسان هستند.
شاید مطالعه این مقالات هم برای شما مفید باشد:
- اضافه کردن عنصر به لیست در پایتون (کد + آموزش تصویری)
- لیست در پایتون (انواع، کد و نحوه استفاده و …)
- تبدیل انواع داده در پایتون (آموزش کامل، ساده و قدم به قدم)
- نوع داده رشته ای در پایتون (آموزش با مثال عملی)
- انواع متغیرها در پایتون (با مثال ساده)
- عملگرها در پایتون (عملگر توان، باقیمانده و تقسیم صحیح به زبان ساده)
- نحوه کامنت کردن در پایتون (آموزش تصویری کامنت گذاری)
نتیجهگیری
ب.م.م در پایتون یک ابزار کلیدی در راستای بهینهسازی محاسبات ریاضی و پردازش دادهها در برنامهنویسی به شمار میرود. تسلط بر روشهای مختلف مانند تابع gcd در ماژول math و الگوریتم اقلیدسی که از طریق تمرین به دست میآید، همراه با شناخت چالشهای رایج و راهکارهای برطرف کردن آنها، باعث افزایش کارایی کدها میشود.
در پروژههای پیچیدهتر نیز، میتوانید از کتابخانههایی مانند NumPy و SymPy برای افزایش دقت و سرعت محاسبات استفاده کنید و مسائل اعداد بزرگتر را حل کنید. به یاد داشته باشید درک این مفهوم نه تنها در حل مسائل ریاضی، بلکه در بهینهسازی الگوریتمها هم نقش مهمی دارد.
سوالات متداول
1. تفاوت بین استفاده از تابع gcd و پیادهسازی الگوریتم اقلیدسی چیست؟
تابع gcd در ماژول math یک راه ساده و سریع برای محاسبه ب.م.م است، در حالی که پیادهسازی الگوریتم اقلیدسی امکان کنترل دقیقتر روی فرآیند محاسبه را فراهم میکند و طبعا کمی پیچیدهتر است.
2. چرا باید از ب.م.م در برنامهنویسی پایتون استفاده کنیم؟
ب.م.م در پایتون برای سادهسازی کسرها، یافتن نسبتهای مشترک و بهینهسازی الگوریتمهای ریاضی و پردازش دادهها کاربرد دارد.






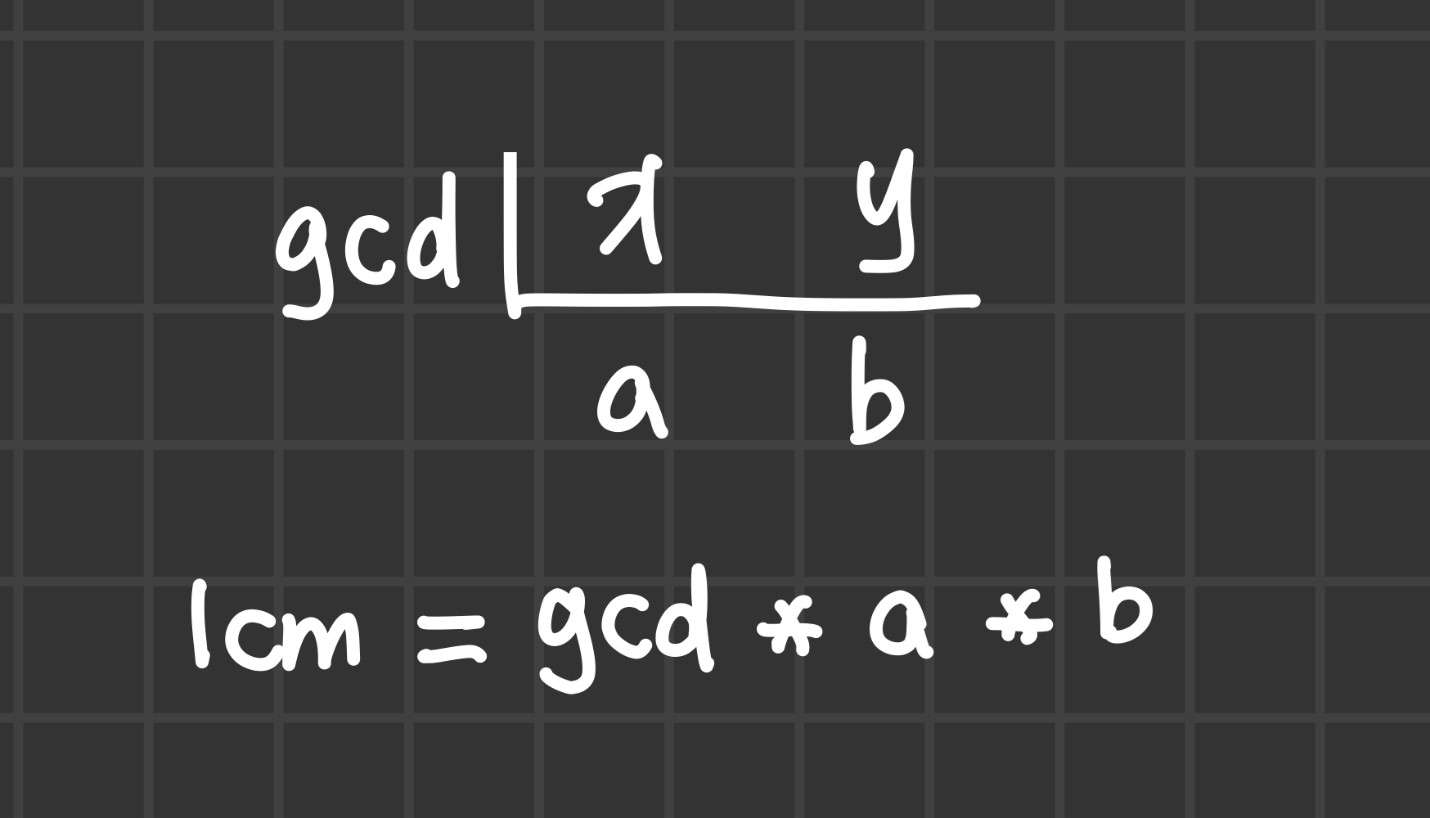






ارسال پاسخ