محاسبه ضرب و تقسیم ماتریس‌ها در متلب+ تصویر(جلسه بیست و چهارم)

در این دوره آنلاین آموزش متلب به صورت رایگان با سری آموزش‌های نرم افزار متلب در خدمت شما هستیم. در واقع آنچه که شما به طور کاملا عملی برای استفاده در انجام پروژه متلب نیاز دارید در این جلسات ارائه خواهد شد.

در جلسه بیست و سوم درباره نحوه استفاده از نحوه محاسبه جمع و تفریق ماتریس‌ها در متلب صحبت کردیم. اگر میخواهید با نحوه محاسبه ضرب و تقسیم ماتریس‌ها در متلب آشنا شوید این مطلب را با دقت تا انتها بخوانید.

ضرب ماتریس‌ در متلب

فرض کنید که یک ماتریس به نام ماتریس A داریم. این ماتریس به صورت زیر تعریف می‌شود که دارای دو سطر و دو ستون است.

سطر به انگلیسی به معنی row و ستون به معنی column است.

یعنی یک ماتریس ۳×۲ است و فرض کنید که یک ماتریس دیگری به نام ماتریس B داریم که این ماتریس دارای سه سطر و دو ستون است که به صورت زیر تعریف شده است و همه‌ی اعداد آن فرد هستند. این ماتریس هم دارای سه سطر و دو ستون است.

اگر این دو ماتریس را در هم ضرب کنیم، چه اتفاقی می‌افتد؟ یعنی ماتریس A را در ماتریس B ضرب کنیم. مشاهده می‌کنیم که یک ماتریس را به ما داد که یک ماتریس ۲×۲ است یعنی ۲ سطر و ۲ ستون دارد.

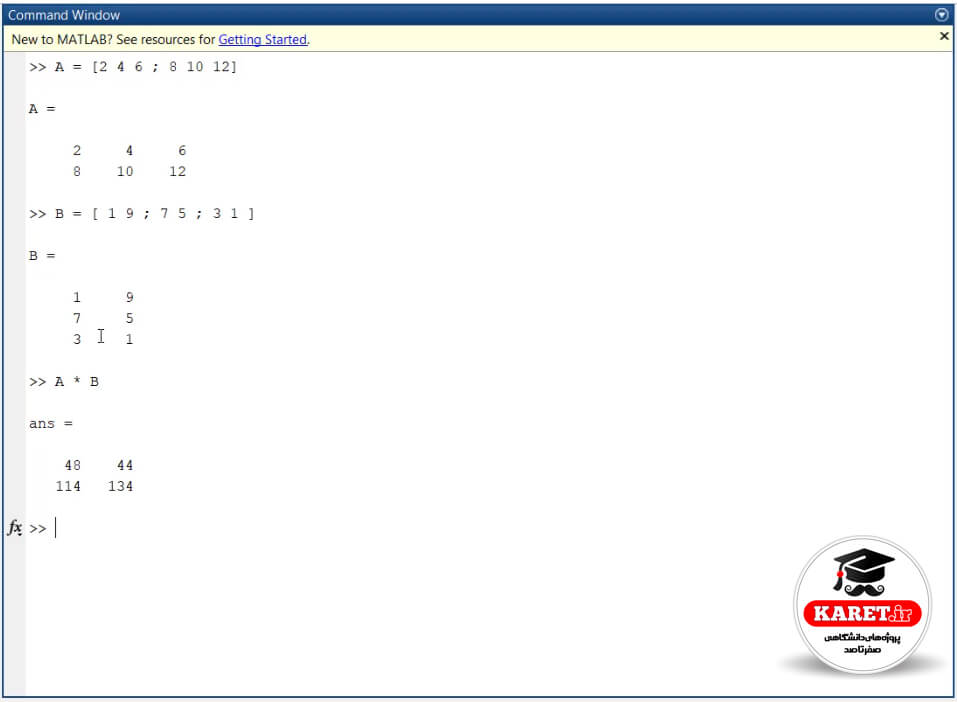
ضرب ماتریس‌ها را اگر در خاطر داشته باشید، سطر اول ماتریس A در ستون اول ماتریس B ضرب می‌شود و در درایه‌ی  ماتریس حاصل‌ضرب قرار می‌گیرد. سپس سطر اول ماتریس A  در ستون دوم ماتریس B ضرب می‌شود و در درایه‌ی  ماتریس حاصل‌ضرب قرار می‌گیرد. سپس سطر دوم ماتریس A  در ستون اول ماتریس B ضرب می‌شود و در درایه‌ی  ماتریس حاصل‌ضرب قرار می‌گیرد. سپس سطر دوم ماتریس A  در ستون دوم ماتریس B ضرب می‌شود و در درایه‌ی  ماتریس حاصل‌ضرب قرار می‌گیرد.

ضرب سطر در ستون هم برای درایه‌ی اول به صورت زیر است و برای بقیه سطر و ستون‌ها به طور مشابه صورت می‌گیرد:

این یک فرمول خاصی دارد که در اینجا برایتان توضیح می‌دهم. یک ماتریس ۳×۲ یک ماتریس ۲×۳ داشتیم که به ما یک ماتریس ۲×۲ داده است.

برای این‌که ماتریس‌ها بتوانند در هم ضرب شوند، همیشه باید تعداد ستون‌های ماتریس اول با تعداد سطرهای ماتریسی دوم با هم برابر باشند. در اینجا چون هر دو ۳ هستند و با هم برابرند، پس ماتریس حاصل‌ضرب ما یک ماتریس ۲×۲ است.

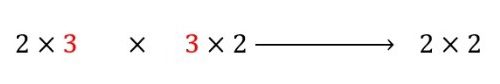
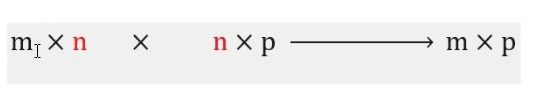
حاصل ضرب یک ماتریس  در یک ماتریس  یک ماتریس   است.

تا زمانی که n و n با هم برابر باشند، دو ماتریس می‌توانند در هم ضرب شوند.

اما در برنامه متلب می‌خواهیم یک توضیحی بنویسیم، قبل از آن یک علامت % قرار می‌دهیم و به صورت زیر  می‌نویسیم:

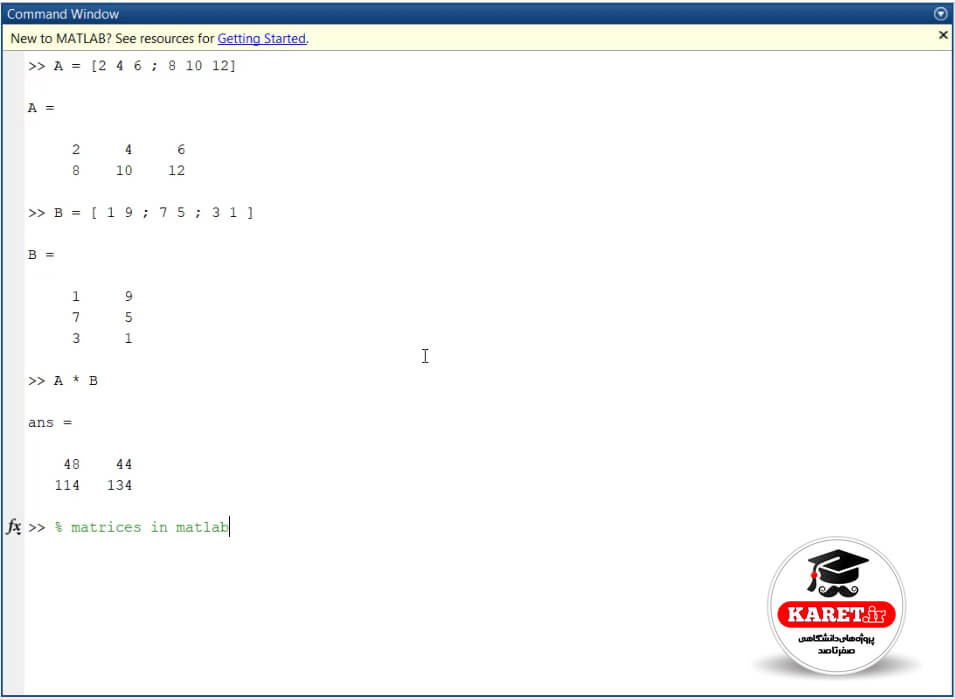
مشاهده می‌کنیم که نوشته به رنگ سبز درآمده است. وقتی که یک علامت % در قسمت command window برنامه متلب قرار می‌دهید، این یعنی این‌که برای خودتان دارید یک note می‌نویسید و هیچ تأثیری در برنامه‌نویسی ما ندارد.

مثلاً در زبان java script دو تا / (slash) را که قرار دهیم، این معنی را برای ما می‌دهد اما در متلب با علامت درصد می‌توانیم این کار را انجام دهیم. در برنامه‌نویسی‌ها با زبان‌های دیگر شاید به صورت‌های مختلفی این کار را انجام می‌دهند.

در workspace ما value (مقدار) ماتریس A را برایمان مشخص کرده است که [2,4,6; 8,10,12] بوده است.

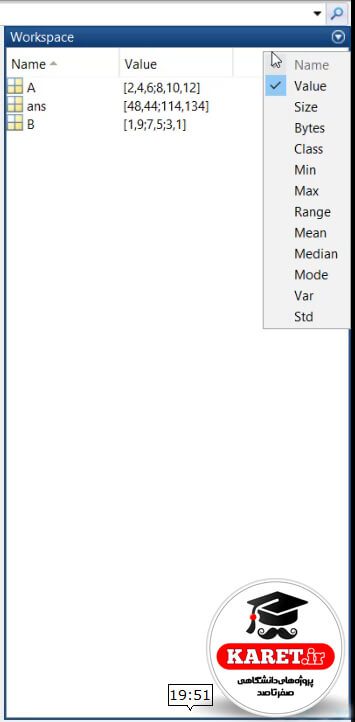
اگر در این قسمت یک کلیک راست انجام دهیم، به طور مثال اگر size آن را بخواهیم، برای ما size آن را هم نمایش می‌دهد که به طور مثال ۲×۳ است.

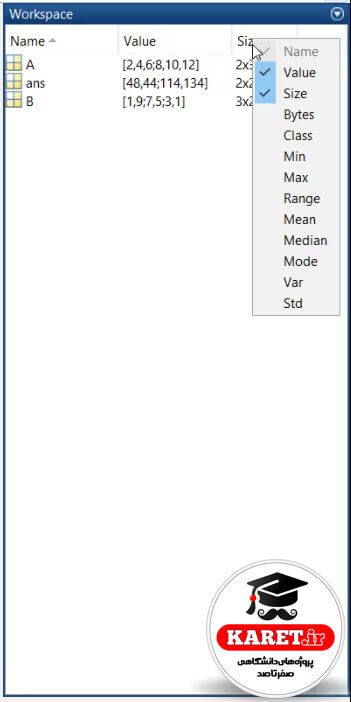
مثلاً ans که ضرب A و B بود، ۲×۲ شده است.

حال که دیگر size را لازم نداریم، تیک آن را برمی‌داریم.

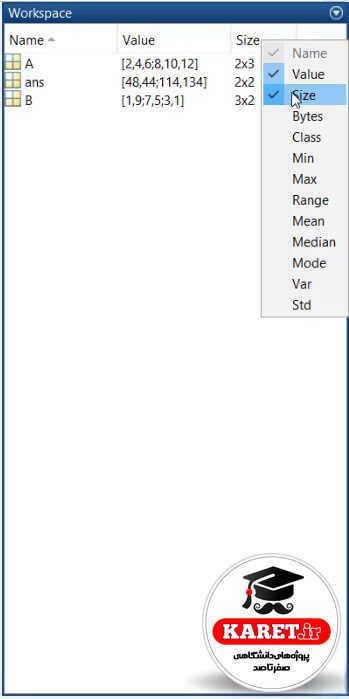
به طور مثال اگر بخواهیم ببینیم مقدار مینیمم (کمترین مقدار) در ماتریس A،B و جواب آن چیست.

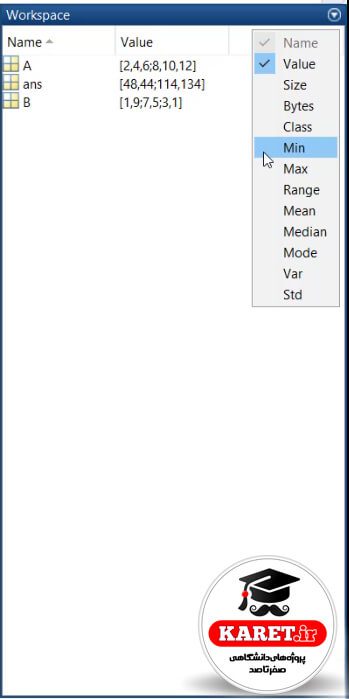
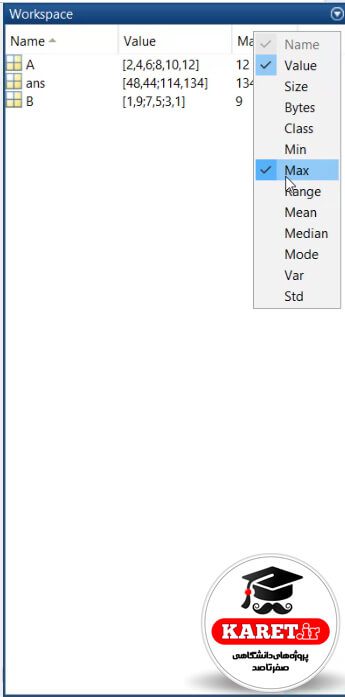
از این طریق کمترین مقدار را برای ما به دست می‌آورد. برای به دست آوردن بیشترین مقدار هم Max را از بین گزینه‌ها انتخاب می‌کنیم.

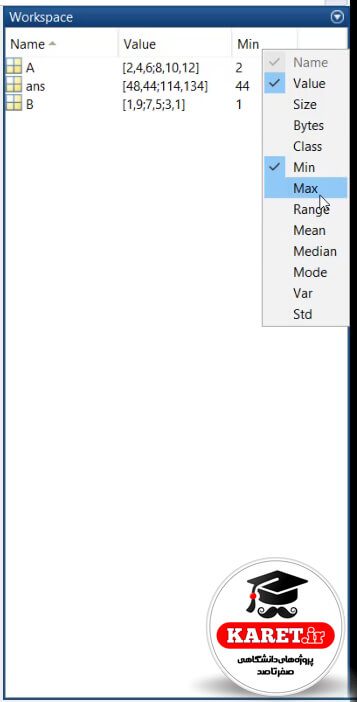
که مشاهده می‌کنیم، مقادیر آن ۱۲ و ۱۳۴ و ۹ هستند. بیشترین مقدار در حاصل‌ضرب ۱۳۴ و در ماتریس B مقدار ۹ بوده است.

تیک هر کدام از گزینه‌ها که لازم نداشته باشیم را برمی‌داریم.

اکنون یک مثال بیان می‌کنیم که قضیه به خوبی توضیح داده شود و این‌که نکته‌ای که در ضرب ماتریس‌ها وجود دارد را هم بیان کنیم.

فرض کنید که یک شخصی برای دویدن هر روز از خانه‌اش بیرون می‌رود و زمان‌هایی که می‌گذارد را اگر با time نشان دهیم، برای مثال یک روز نیم ساعت وقت گذاشته است و یک روز ۷/۰ ساعت وقت گذاشته است و یک روز دیگر هم همان نیم ساعت وقت گذاشته است و یک روز ۱ ساعت و ۱۰ دقیقه وقت گذاشته است و یک روز هم مثلاً ۲ ساعت وقت گذاشته است.

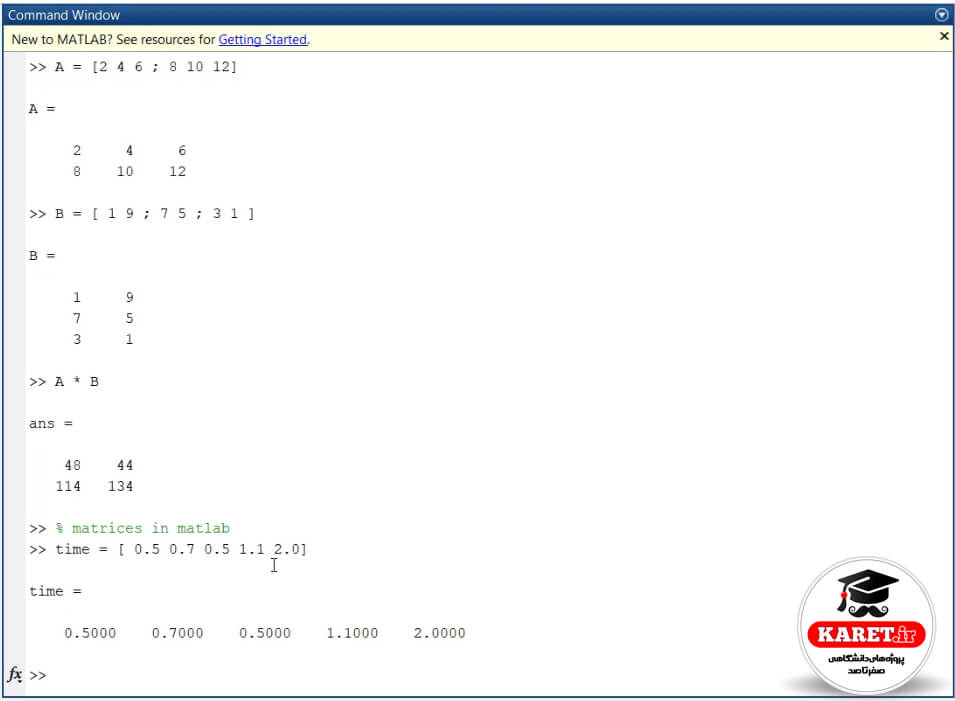
این‌ها timeهای ما هستند.

می‌خواهیم ببینیم که در روز با چه سرعتی دویده است. سرعت به انگلیسی velocity می‌شود که با حرف v نشان می‌دهند.

به طور مثال سرعت روز اول آن ۱۵ متر بر ثانیه بوده است. سرعت روز دوم که مثلاً تندتر دویده است، ۱۶ متر بر ثانیه بوده است و روز سوم ۱۸ متر بر ثانیه بوده است و روز بعد مثلاً مریض شده است، ۱۵ متر بر ثانیه دویده است و روز آخر هم کرونا گرفته است و مثلا ۱۴ متر بر ثانیه دویده است. این سرعت آن شخص است.

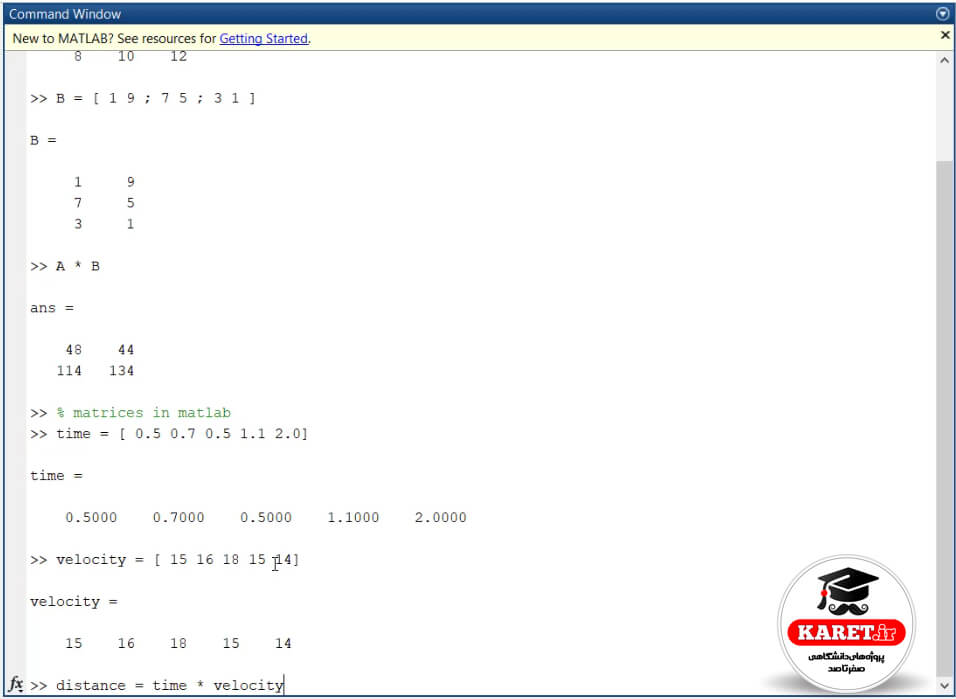
حال می‌خواهیم ببینیم که مسافتی که این شخص رفته است، چقدر بوده است. فرمول مسافت چه بود؟ زمان ضربدر سرعت که در خط آخر تصویر فوق نشان داده شده است.

Distance یا مسافت برابر است با زمان ضربدر سرعت. که این همان ضرب دو ماتریس شده است. زیرا در اینجا نیز دو ماتریس داریم. یک ماتریس ۵×۱ و یک ماتریس ۵×۱ دیگر هم در اینجا داریم.

پاسخ حاصل‌ضرب را در تصویر زیر خواهیم دید.

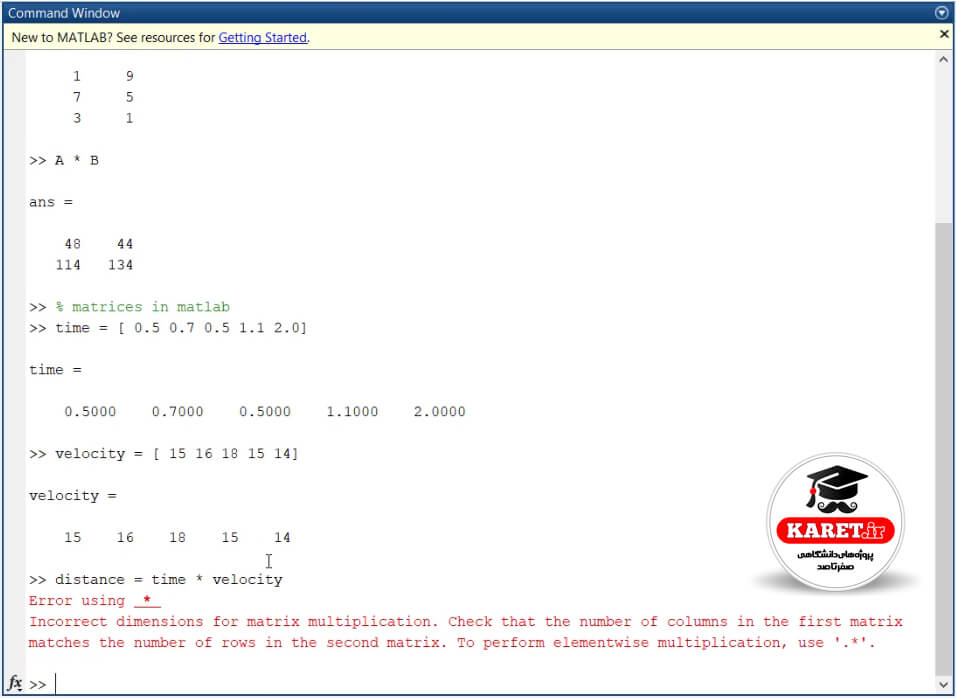
جوابی به ما نداده است. چرا؟ دلیل دارد و دلیل آن را هم قبلاً گفتیم.

در اینجا ما دو ماتریس ۵×۱ داشتیم که زمان و سرعت را به ما نشان می‌داد. همان‌طور که مشاهده می‌کنید ۵ با ۱ برابر نیست. زیرا گفته بودیم که n باید با n برابر باشد.

پس error دریافت می‌کنیم. حال می‌خواهیم در اینجا این ضرب را حتما انجام دهیم و جواب را می‌خواهیم. یک مسئله‌ای برای ما پیش آمده است که جواب آن را می‌خواهیم. چه کاری باید انجام دهیم؟ راه حل دارد و راه حل آن نیز استفاده از element wise multiplication است.

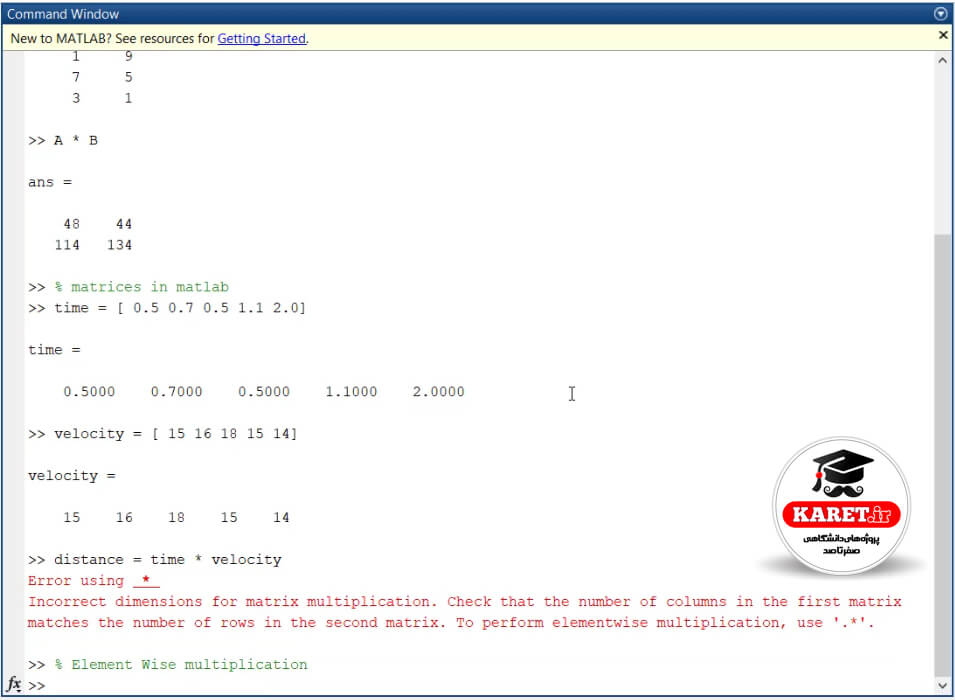
و این راه حل ماست. حال چگونه باید آن را اجرا کنیم؟ با گذاشتن یک dot (نقطه) قبل از ضرب یا ماتریس دیگر به این موارد اصلاً توجهی نمی‌کند و ضرب را انجام می‌دهد که اگر بخواهیم ببینیم به صورت زیر باید نوشته شود:

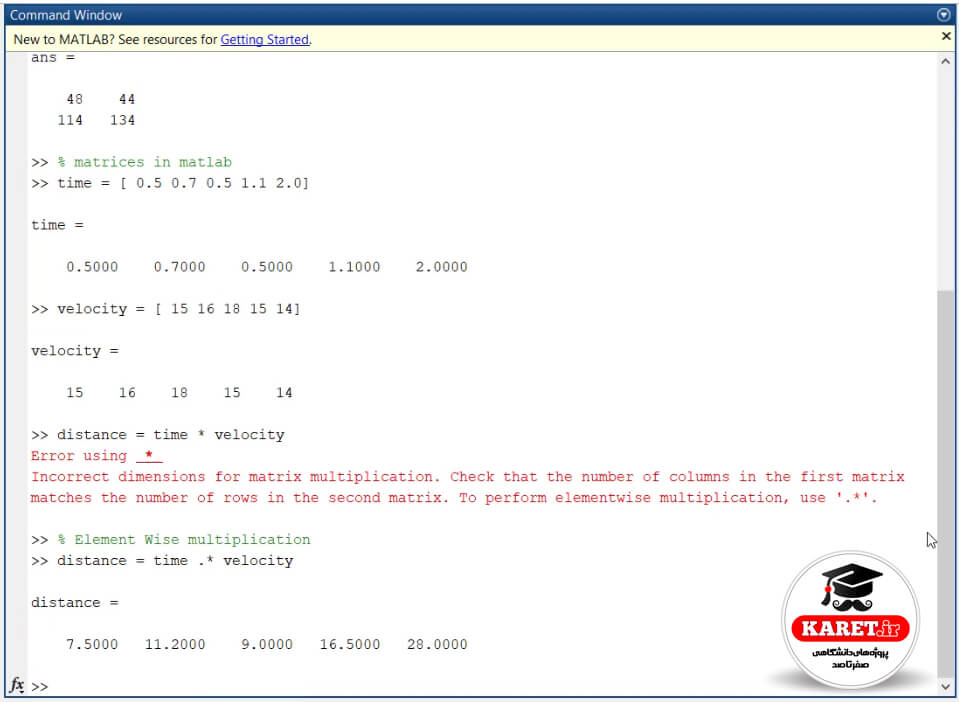
مشاهده کردید که به سادگی ضرب شده است و مسافتی که طی کردیم، ۵/۷، ۲/۱۱، ۹، ۵/۱۶ و ۲۸ را به ما داده است.

اما فقط در ضرب به این صورت نیست. شما مثلاً اگر این تقسیم را هم انجام می‌دادید، به همین صورت می‌شد. برای مثال اگر می‌خواستیم سرعت را به دست آوریم و سرعت را نداشتیم و سرعت برای ما مجهول بود، به همین صورت بود و باید dot قرار می‌دادیم و مثلاً اگر v را می‌خواستیم، باید به صورت زیر می‌نوشتیم:

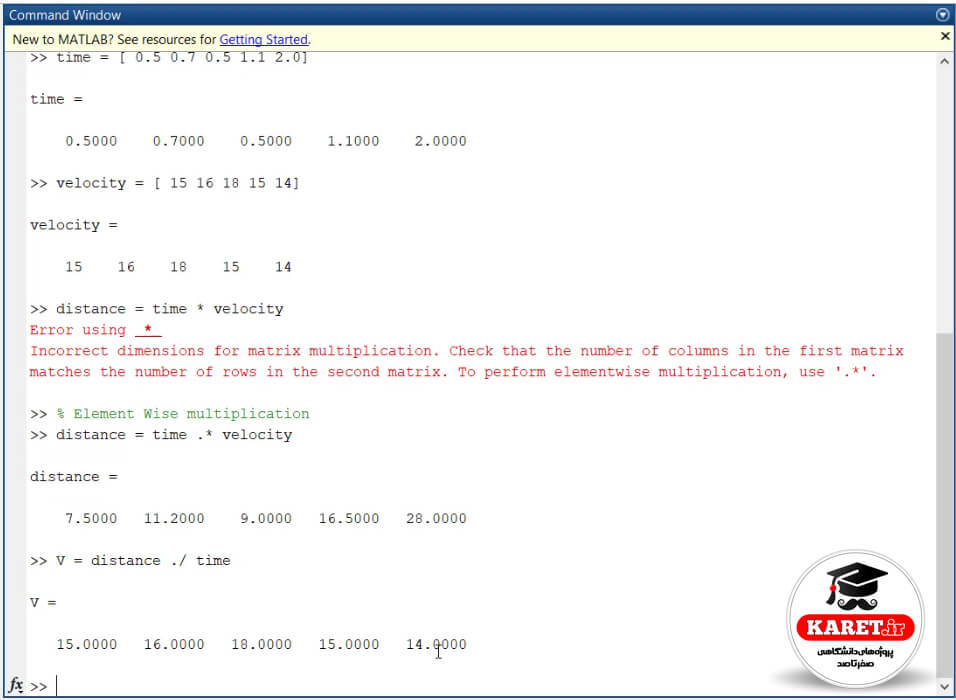
که v را به ما می‌داد که همان ۱۵ و ۱۶ و ۱۸ و ۱۵ و ۱۴ بوده است. حال فرض کنید که می‌خواهیم انرژی را هم محاسبه کنیم اگر به یاد داشته باشید، انرژی جنبشی را با  نشان می‌دادیم که مخفف kinetic energy به معنی انرژی جنبشی است و فرمول آن به صورت  است. حال برای به دست آوردن این فرمول ابتدا باید جرم را داشته باشیم. فرض می‌کنیم جرم باشد.

گفتیم انرژی جنبشی با فرمول زیر به دست می‌آید:

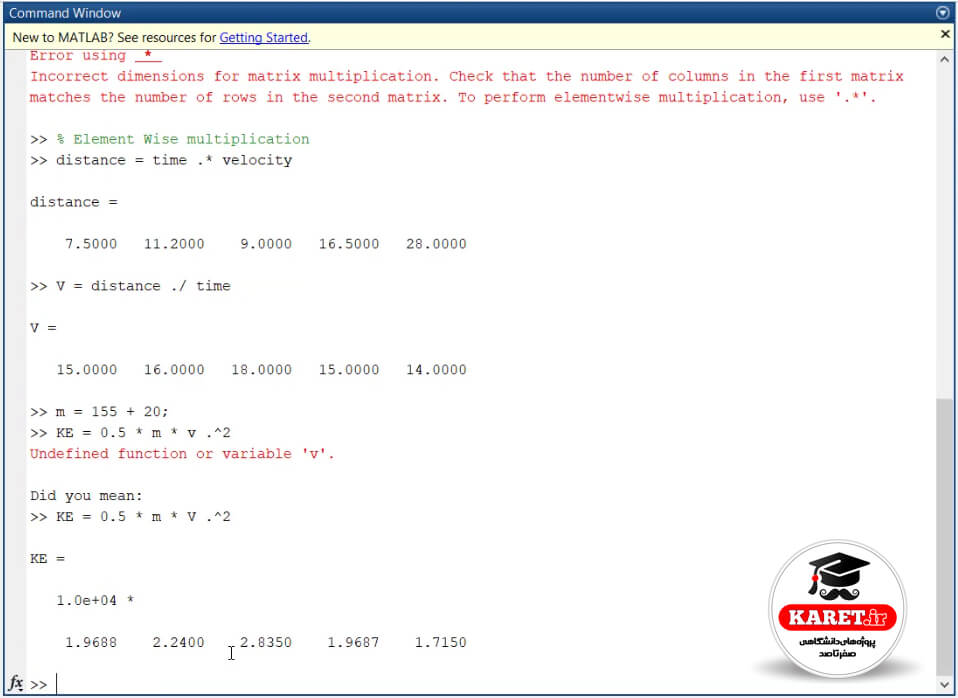
اگر توجه کنید، ما در اینجا ضرب به کار بردیم، زیرا m خودش یک ماتریس ۱×۱ است و این هم یک ماتریس ۵×۱ است. nهای آنها با هم برابرند و نیازی به dot نداریم.

موضوع دیگری که در جلسات قبلی به شما توضیح دادم، مبحث extracting elements parametric submatrices from an existing matrix (یعنی جداسازی یک المان یا ماتریس یا به طور مثال زیرماتریس از یک ماتریسی که وجود دارد)، بوده است.

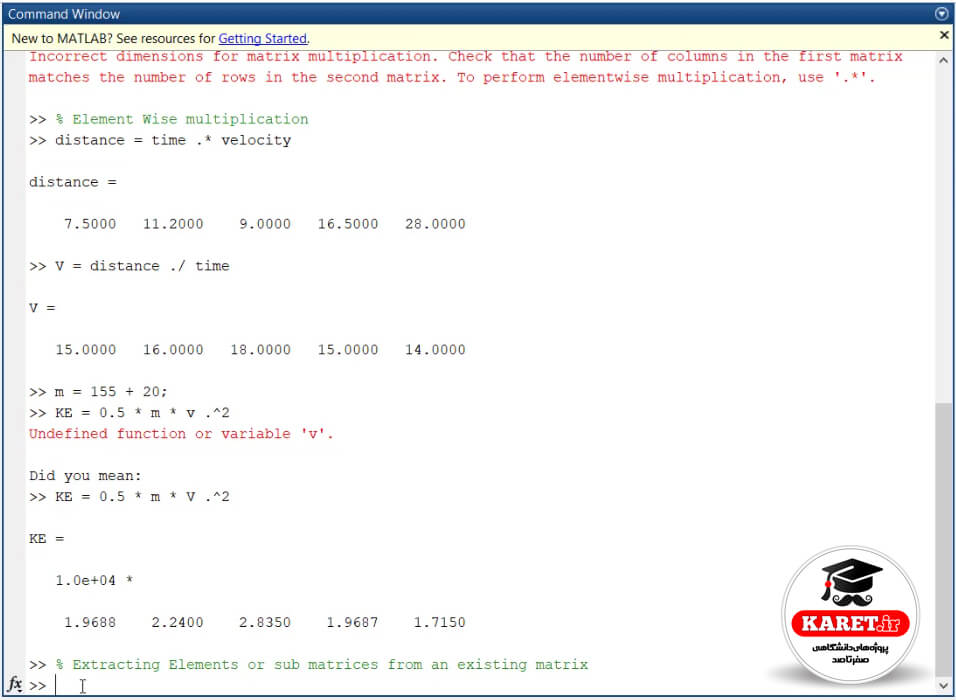
این مبحث نیز مبحثی بود که من کمی راجع به آن برایتان توضیح دادم و فکر می‌کنم که کامل هم آن را توضیح دادم.

اگر بخواهیم یک مروری داشته باشیم، فرض کنید ما ماتریس C را داریم و اعضای آن  باشند. فرض کنیم که این ماتریس را داریم که یک ماتریس ۳×۳ و دارای سه سطر و سه ستون است.

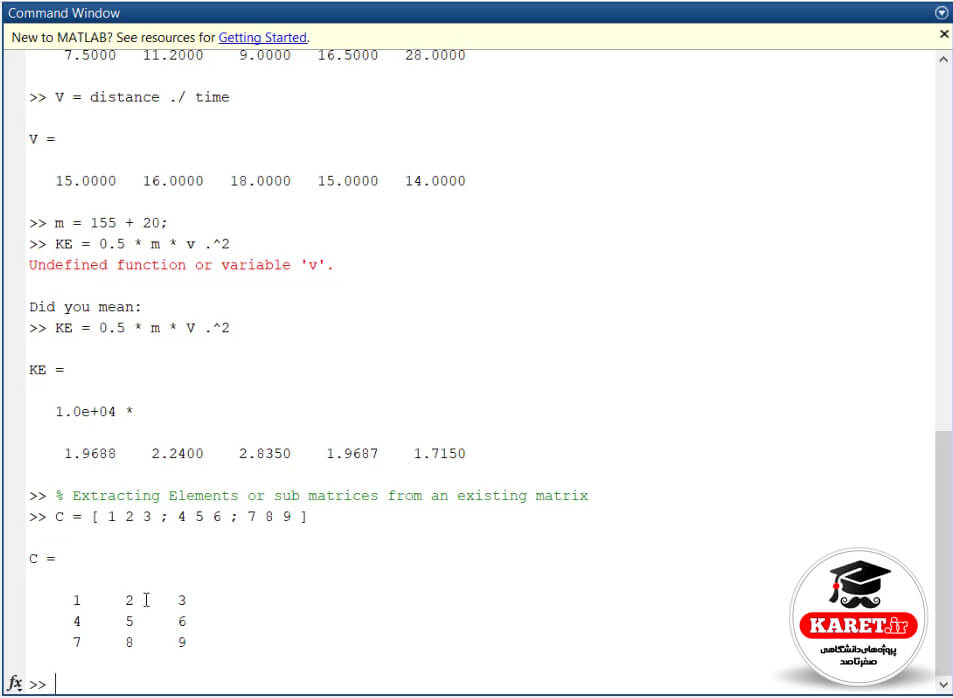
حال در اینجا چه می‌خواهیم؟ مثلاً در سطر یک و ستون دو ۲ را می‌خواهیم و در واقع می‌خواهیم یک عدد را extract کنیم. به این کار single element extraction می‌گویند. یعنی این‌که یک المان را از این ماتریس جدا کنیم.

ما ۲ را می‌خواهیم. عدد ۲ در سطر یک و ستون دو قرار دارد. به صورت زیر می‌نویسیم:

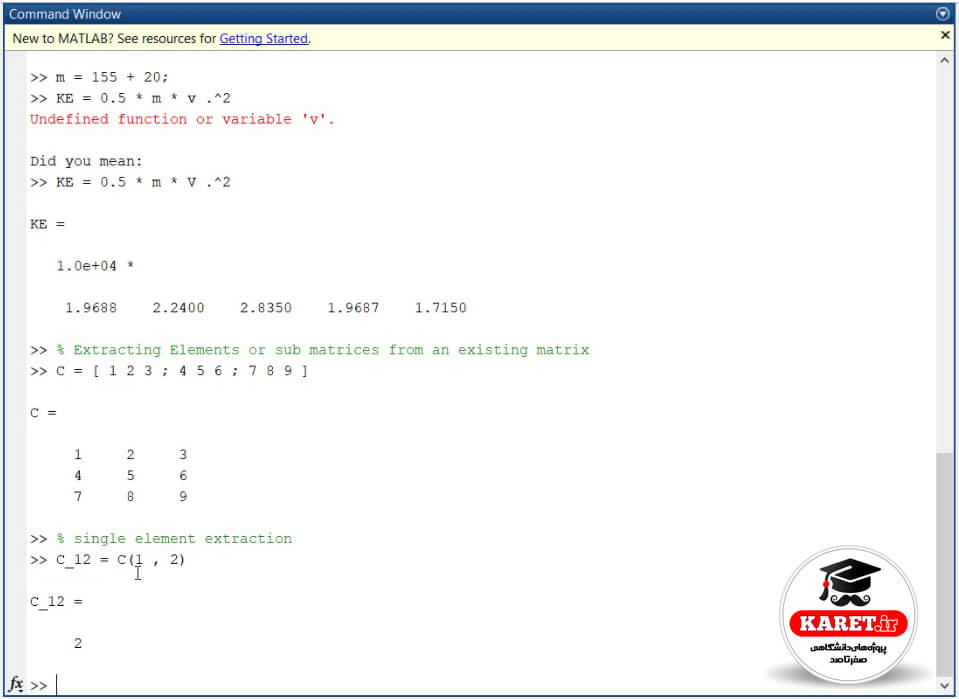
که مشاهده می‌کنیم که به راحتی عدد ۲ را به ما برگرداند.

حال اگر به طور مثال بخواهیم یک سطر یا ستون کامل را از ماتریس (extract) جدا کنیم، به صورت زیر نوشته می‌‌شود:

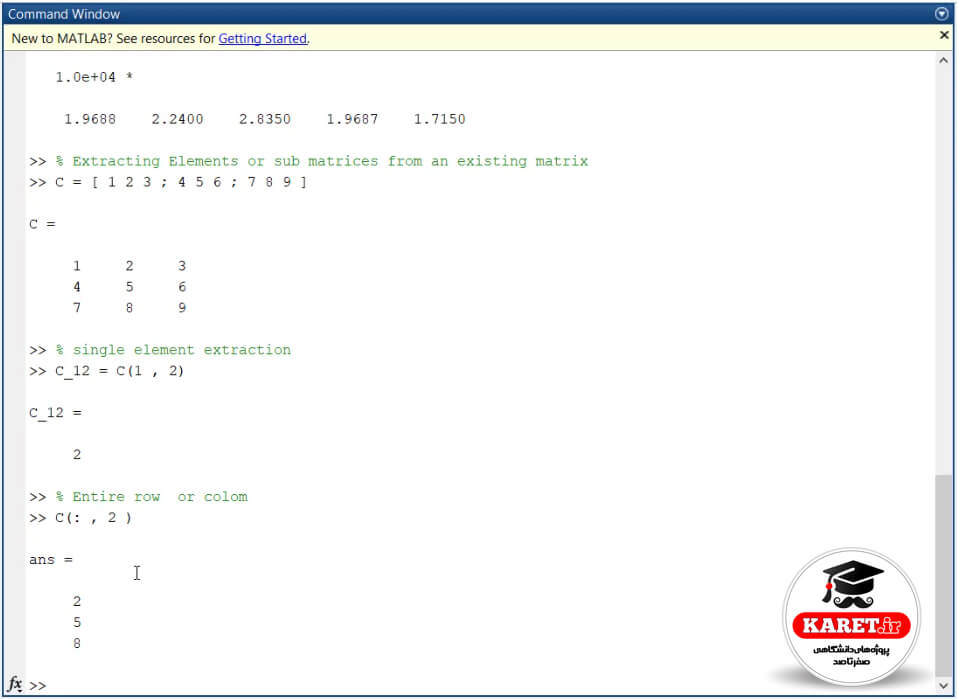
برای این کار به صورتی که در تصویر فوق نوشته شده است، عمل  می‌کردیم. مشاهده می‌کنیم که برای ما ستون دو را به طور کامل استخراج کرده است. ستون دو شامل اعداد ۲ و ۵ و ۸ است. حال اگر سطر دو را می‌خواستیم استخراج کنیم، به صورت ” C (2 , : ) ” تایپ می‌کردیم.

به طور مثال سطر ۳ را می‌خواهیم استخراج کنیم. سطر ۳ به صورت زیر جدا می‌شود:

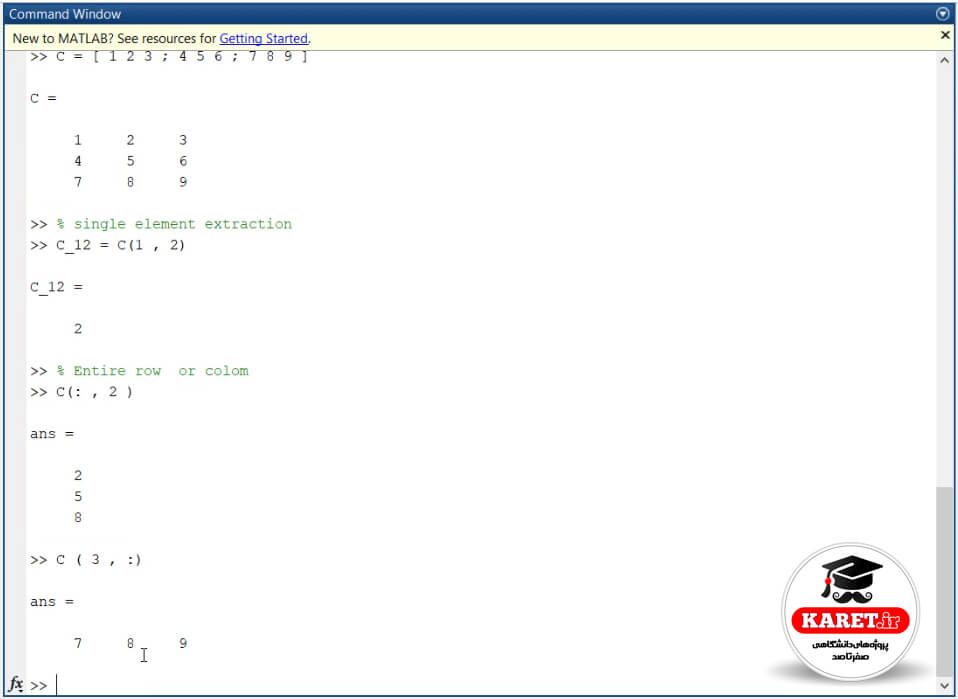
که همان‌طور که مشاهده می‌کنید، سطر ۳ را استخراج کرد و بیرون آورده است. اما سومین موردی که فکر می‌کنم در مورد آن توضیح نداده‌ام، sub matrix است. یعنی یک ماتریس را بخواهیم از آن استخراج کنیم. خودتان کمی روی آن فکر کنید که با استفاده از مطالبی که تا اینجا بیان کردیم، چگونه می‌توانید این کار را انجام دهید؟ برای مثال می‌خواهیم که از این ماتریس ۳×۳ ماتریس ۲×۲  را ستخراج کنیم و بیرون بیاوریم. به این صورت انجام می‌شود:

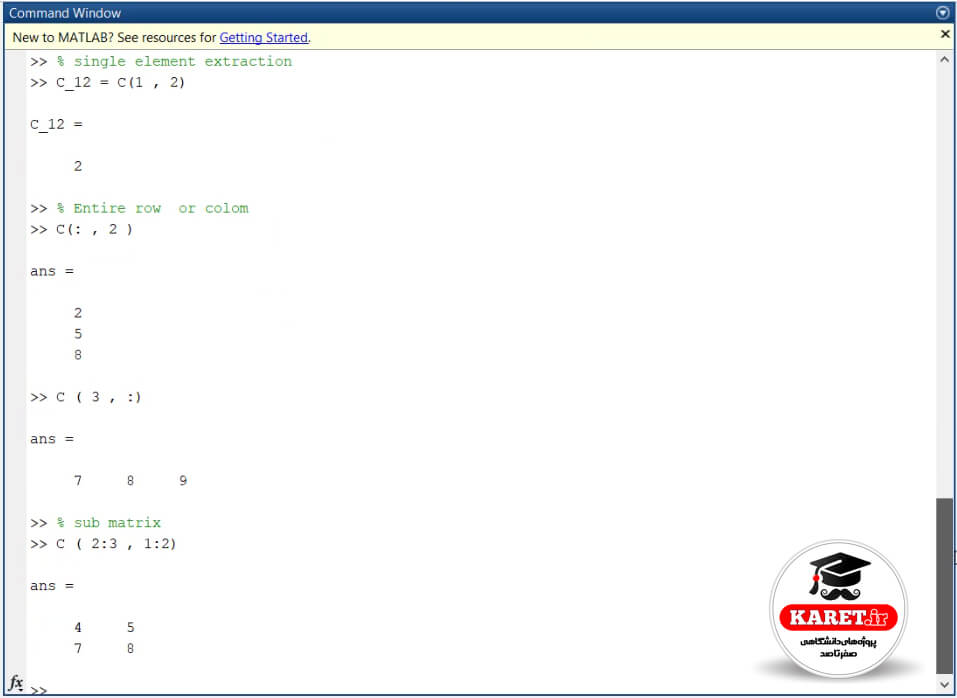
همان‌طور که مشاهده می‌کنید دقیقاً همان ماتریس را برای ما استخراج کرده است. این ماتریس را از ماتریس اصلی C بیرون آورده است. چگونه این کار انجام شده است؟ در فرمول بالا 2:3 به معنی سطرهایی است که شروع می‌شود (start rows to end) یعنی از سطر ۲ تا ۳. و 1:2 یعنی از ستون یک تا دو را می‌خواهیم.

به طور کلی یعنی از سطر ۲ تا ۳ و از ستون ۱ تا ۲ را برای ما بیرون می‌کشد و دقیقا همان ماتریسی را می‌دهد که می‌خواستیم. به این صورت اکسترکت انجام شده است.

نکته‌ی دیگری که می‌خواهم بیان کنم، این است که قبلا گفتیم به طور مثال وقتی [3: 0.25 : 6] را نوشتیم، با قدرنسبت 0.25 جلو می‌رود و از ۳ تا ۶ به جلو می‌رود.

اگر به جای 0.25، قدرنسبت ۱ قرار دهیم، یکی یکی به جلو می‌رود.

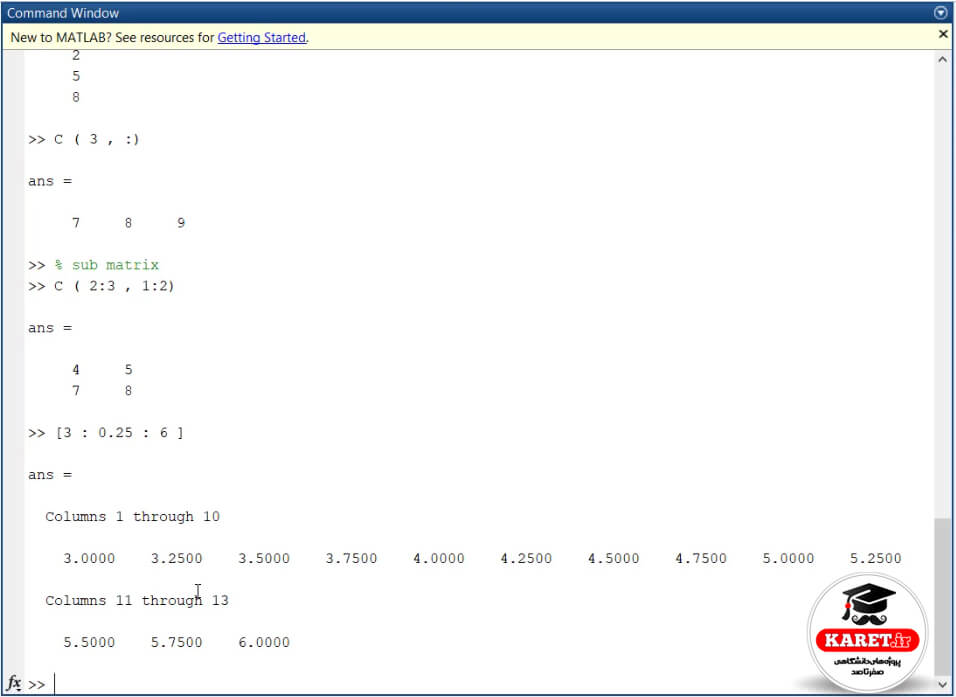
حال می‌خواهیم یک نکته‌ی دیگری ر‌ا نیز بیان کنیم که linearlyspace است. در اینجا یک دستوری به نام linespaced داریم که به طور مثال به صورت زیر می‌نویسیم:

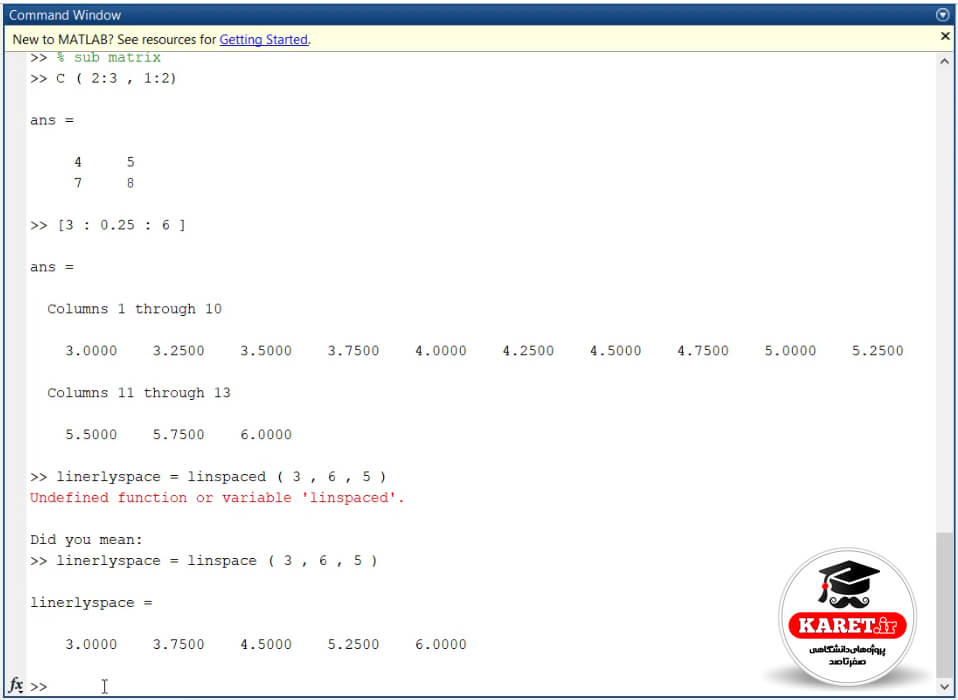
همان‌طور که در تصویر فوق مشاهده می‌کنید، به صورت linspace باید می‌نوشتیم و linespaced املای صحیح آن نبوده است و حرف d اضافه بوده است.

این می‌گوید که بین ۳ تا ۶، پنج عدد بنویسد. و خودش به دلخواه جدا کرده است.

حال به طور مثال ۱۵ تا عدد بین ۳ تا ۶ می‌خواهیم بنابراین به صورت زیر می‌نویسیم:

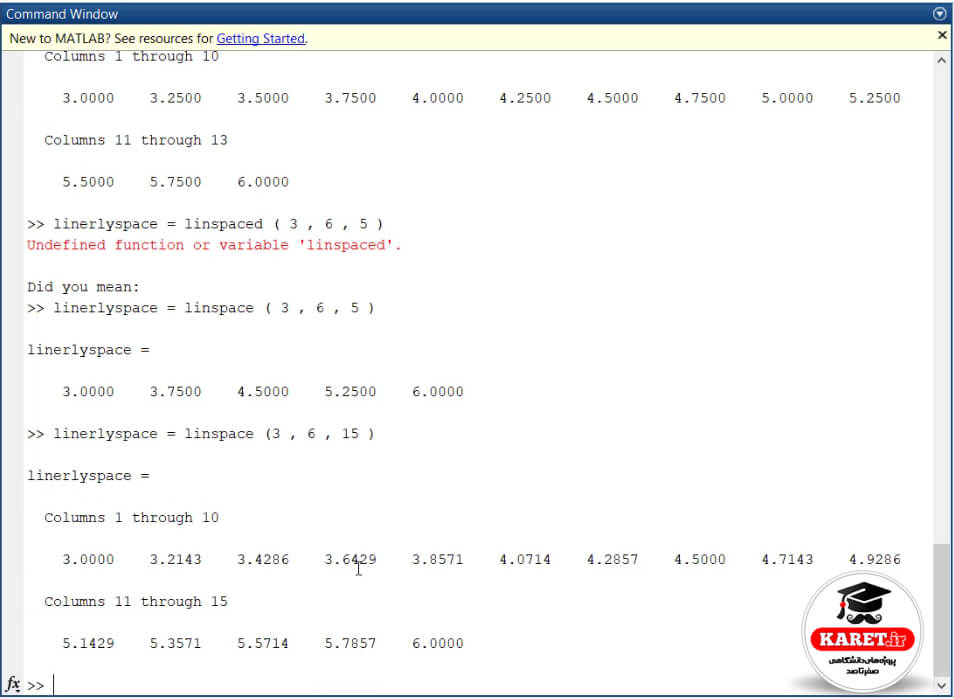
که ۱۵ عدد به ما داده است.

دستور آخری که می‌خواهم توضیح دهم، فرض کنید ما چنین چیزی داریم و می‌خواهیم ببینیم اعضای آن چند تا بوده است. مثلاً این تعداد ۱۵ تا نبوده است و ۱۲۰۰ تا بوده است. در این حالت نمی‌توانم آن را یکی یکی بشماریم. بنابراین به صورت زیر می‌‌نویسیم:

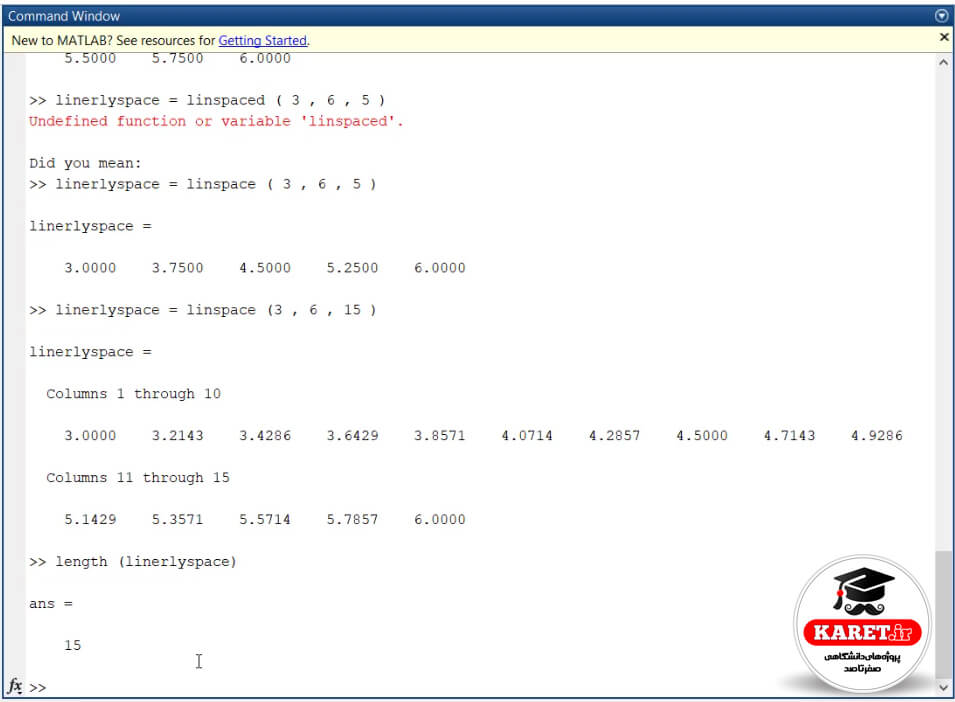
که در جواب به ما گفته است این ۱۵ عدد است.

تقسیم ماتریس‌ها در متلب

حال می‌خواهیم در مورد تقسیم ماتریس‌ها صحبت کنیم و در مورد آن توضیح دهیم.

تقسیم در متلب می‌تواند با علامت‌های / یا نشان داده شود. در تمام زبان‌های برنامه‌نویسی هم تا جایی که مشاهده کردم، به همین صورت است و این که معنی تقسیم در ماتریس به صورت زیر توضیح داده می‌شود:

در B/1 به معنی معکوس B است. معکوس 1/B نیز همان B است. و معکوس را با نماد B به توان منفی 1 نشان می‌دهند که این transpose یا ترانهاده نیست. در مورد transpose یا ترانهاده قبلاً توضیح دادم که چیست.

پس ما در واقع ماتریس‌ها را تقسیم نمی‌کنیم. بلکه به جای آن ماتریس را در معکوس ماتریس دیگر ضرب می‌کنیم.

به این نکته توجه داشته باشید که همانند جمع و تفریق ماتریس‌ها، در تقسیم ماتریس‌ها نیز باید ابعاد دو ماتریس با هم برابر باشند. به طور مثال هر دو ۲×۲ یا هر دو ۳×۳ باشند.

اگر پس از خواندن دقیق تمامی مطالب فصل اول باز هم جواب سوال خود را پیدا نکردید میتوانید از طریق ارتباط با پشتیبانی کارت با کارشناسان ما در ارتباط باشید.

در این‌ بیست و چهار جلسه تمام نکات مربوط به فصل اول از آموزش مقدماتی متلب بیان شد. از جلسه‌ی بعدی با فصل دوم از این آموزش در خدمت شما خواهیم بود.

در صورتی که شما پس از خواندن محتوای جلسات قبلی و این بخش که به ساده‌ترین زبان ممکن درباره‌ی برنامه‌ی متلب و محیط کاربری آن توضیح داده باز هم سردرگم هستید. می‌توانید با برون سپاری انجام پروژه متلب خود به کارشناسان حرفه‌ای کارت پروژه می‌باشد. میتوانید از طریق شماره‌ی 09104503300 با پشتیبانان کارت از طریق پیام یا تماس در ارتباط باشید.

برای کسب اطلاعات بیشتر در مورد متلب میتوانید به مقاله آموزش متلب مقدماتی مراجعه کنید.