در این دوره آنلاین آموزش متلب به صورت رایگان با سری آموزشهای نرم افزار متلب در خدمت شما هستیم. در واقع آنچه که شما به طور کاملا عملی برای استفاده در انجام پروژه متلب نیاز دارید در این جلسات ارائه خواهد شد.
آموزش نحوه محاسبه دترمینان ماتریس در متلب
جلسه گذشته به آموزش نحوه استفاده از دستور trace در متلب پرداختیم و گفتیم که چگونه میتوانیم مجموع عناصر قطر اصلی ماتریس در متلب را محاسبه کنیم. این جلسه را با پرسشی آغاز میکنیم.
به نظر شما چگونه میتوان حاصلضرب اعضای قطر اصلی را به دست آورد؟ دترمینان ماتریس عدد مخصوصی است که برای ماتریسهای مربعی محاسبه میشود.
ماتریس آرایش منظمی از اعداد است که در سطرها و ستونهای معینی ترتیب یافتهاند. دترمینان چه کاربردی دارد؟ اطلاعاتی در مورد ماتریس به ما میدهد که در سیستمهای معادلات خطی کاربرد دارند. همچنین در یافتن معکوس ماتریس و معادلات دیفرانسیل و انتگرال و شرایط بسیاری دیگر به درد ما میخورد. اگر دترمینان ماتریسی مخالف صفر باشد، آنگاه ماتریس معکوسپذیر است. از این رو از طریق دترمینان میتوان مقادیر ویژهی یک ماتریس و یک نگاشت خطی را تعیین کرد. میتوانیم یک نگاشت خطی از آن تعیین کنیم. حال اگر بخواهیم دترمینان را توضیح دهیم، ابتدا یک ماتریس تعریف میکنیم. مثلاً ماتریس را به صورت زیر تعریف میکنیم:
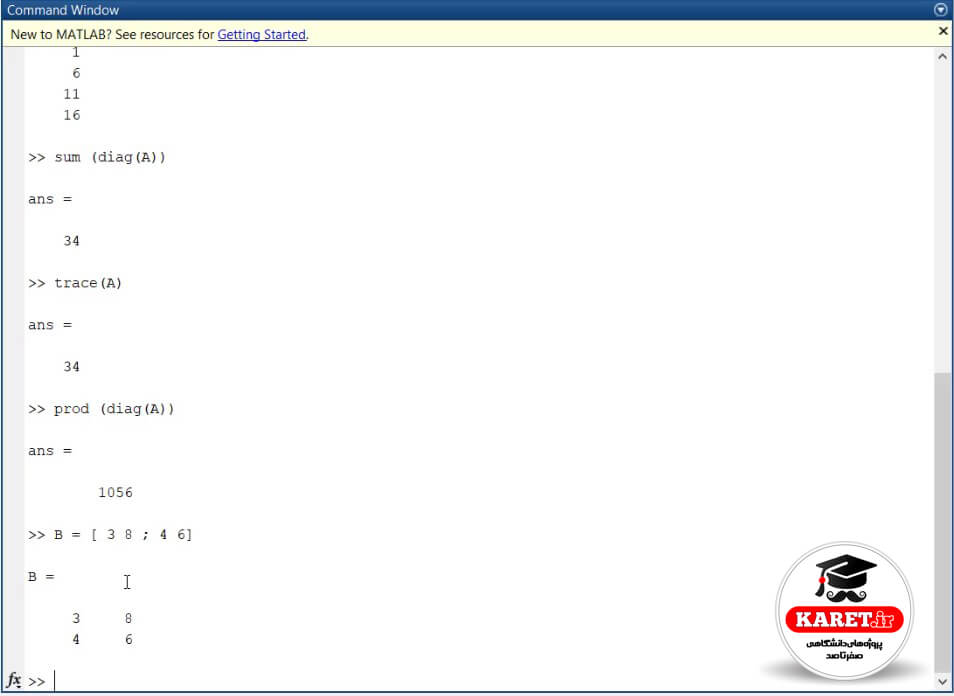
حال میخواهیم محاسبه دترمینان ماتریس در متلب را انجام دهیم. پس به صورت زیر مینویسیم:
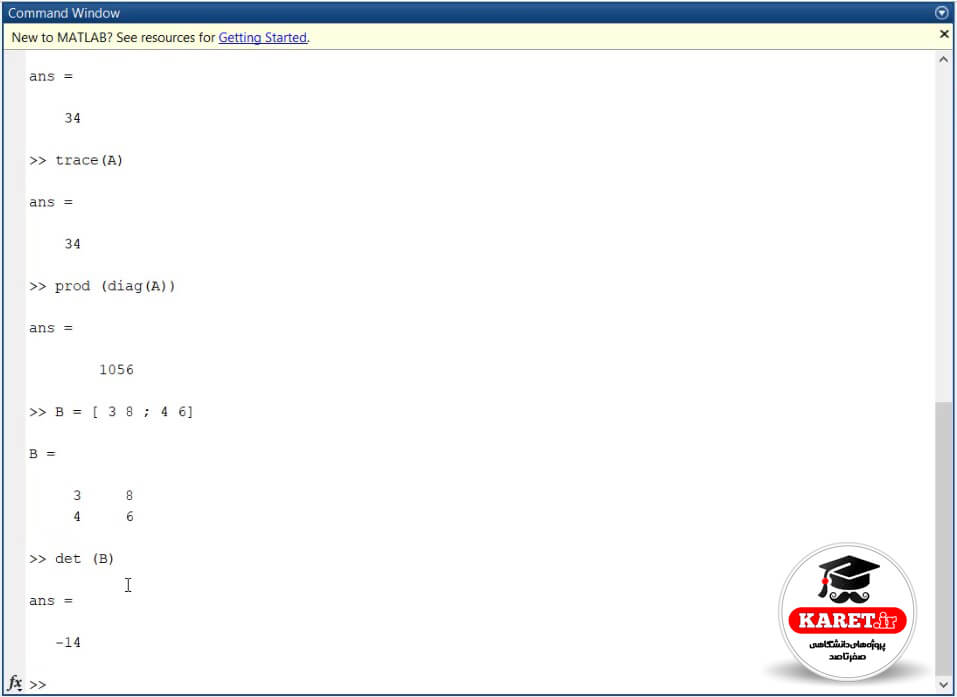
مشاهده میکنیم که جواب ۱۴- شد.
حال به نظر شما چگونه جواب ۱۴- به دست آمد؟
فرض میکنیم که ما برنامهی متلب را نداریم و این ماتریس را به ما دادند و میخواهیم دترمینان آن را به دست آوریم. جواب خیلی ساده است؛ ۳ ضربدر ۶ شده است و سپس منهای (۸ ضربدر ۴) شده است.
(3*6)-(4*8)= -14یعنی ۱۸ منهای ۳۲ شده است که جواب ۱۴- میشود.
دترمینان برای ماتریس ۲×۲ با این فرمول ساده محاسبه میشود.
اما گفتیم که با استفاده از دترمینان میتوان معکوس ماتریسهای ۳×۳ و مراتب بالاتر را نیز محاسبه کرد. حال اینکه یک ماتریس ۲×۲ بود. چگونه میتوان دترمینان ماتریس ۳×۳ را محاسبه کرد؟ البته در ریاضیات اگر بخواهم یک توضیح مختصر بدهم، با استفاده از تصویر زیر به سادگی میتوان توضیح داد که چگونه میتوان دترمینان ماتریس ۳×۳ را به دست آورد.
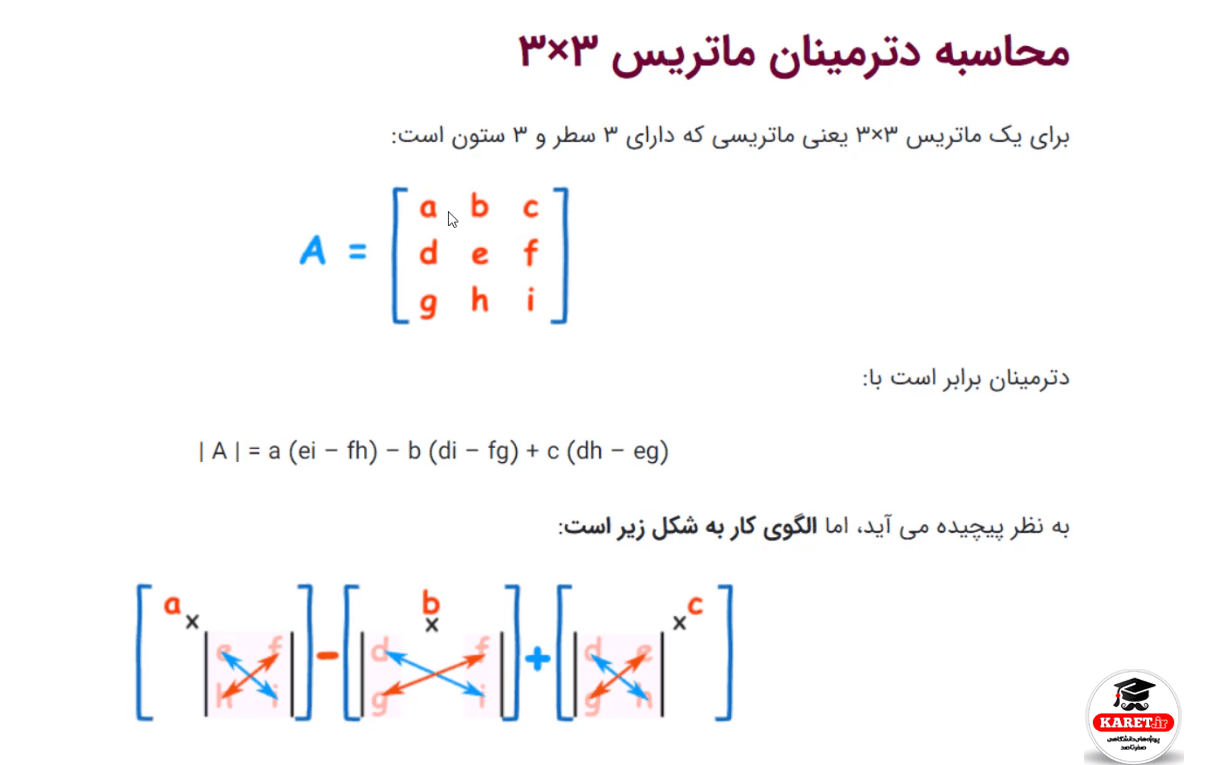
این یک ماتریس است که دقیقاً ۳×۳ است و فرض کنید که هر یک از درایهها دارای یک عدد باشد. ما به صورت کلی دترمینان را به صورت فرمول ارائه شده در تصویر محاسبه میکنیم.
نیازی به حفظ کردن فرمول نیست. a, b, c را در نظر میگیریم که بین آنها یک علامت منها و یک علامت بهعلاوه قرار میدهیم. محاسبهی دترمینان طبق الگو را نیز توضیح دادم که برای ماتریس ۲×۲ به صورت دوتا دوتا است. برای اولی a را مینویسیم که برای مثال عدد ۲ است. ۲ را مینویسیم. عبارت داخل پرانتز روبهروی آن از کجا آمده است؟ ابتدا مشاهده میکنیم که a در سطر یک و ستون یک واقع شده بود. سطر و ستون a را حذف میکنیم. چیزی که باقی میماند، درایههای
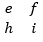
هستند. حال دترمینان این ماتریس ۲×۲ را محاسبه میکنیم که میشود ei – fh
در ادامه فرمول، منهای b را داریم. مشاهده میکنیم که b در سطر اول و ستون دوم واقع شده است. سطر و ستون آن را حذف میکنیم،
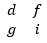
باقی میمانند. دترمینان آن به صورت di – fg محاسبه میشود
و برای مورد آخر یعنی c هم دقیقاً به همین صورت عمل میکنیم. سطر اول و ستون سوم حذف میشوند و
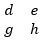
باقی میماند که دترمینان آن به صورت dh – eg محاسبه میشود.
حال اگر هر ماتریسی را به شما بدهند، به راحتی میتوانید به صورت دستی محاسبهی آن را انجام دهید و اگر به برنامهی متلب هم بدهید، که در عرض صدم یا هزارم ثانیه آن را محاسبه میکند.
در جلسهی آینده با آموزش نحوه استفاده از دستور eig در متلب (پیدا کردن بردارهای ویژه) همراه شما خواهیم بود.
در صورتی که شما پس از خواندن محتوای جلسات قبلی و این بخش که به سادهترین زبان ممکن دربارهی برنامهی متلب و محیط کاربری آن توضیح داده باز هم سردرگم هستید. میتوانید با برون سپاری انجام پروژه متلب خود به کارشناسان حرفهای کارت پروژه میباشد. میتوانید از طریق شمارهی 09104503300 با پشتیبانان کارت از طریق پیام یا تماس در ارتباط باشید.
برای کسب اطلاعات بیشتر در مورد متلب میتوانید به مقاله آموزش متلب مقدماتی مراجعه کنید.











ارسال پاسخ